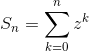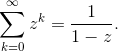Definizione 1.3 ( serie numerica). $$ Sia (a_k)_k∈ℕ una successione in $ℂ$; si chiama serie numerica di termine k-esimo $a_{\mathrm{_k}}$ la successione:

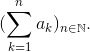
Definiamo inoltre somme parziali della serie:

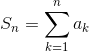
e diciamo che la serie è convergente, divergente o oscillante a seconda che lo sia il .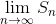

Proposizione 1.4.1. Sia $z\in ℂ$, si dice serie geometrica di ragione z, la serie:

questa converge $\iff \mid z\mid <1$ ed in tal caso