• Home page
• L'infinito e la sua storia
  • Introduzione
  • Segmenti incommensurabili
  • Achille e la tartaruga
  • Paradosso della dicotomia
  • Rettificazione del cerchio
  • Serie numeriche
  • Galilei e l'infinito
  • Infiniti e infinitesimi
  • Infinito moderno
• L'infinito e i frattali
• L'infinito in crittografia
• Bibliografia

1.7 L’infinito moderno

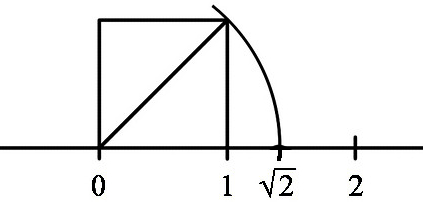
Si deve a Dedekind l’aver risolto due dei maggiori problemi incontrati fino ad allora lavorando con l’infinito potenziale: i numeri irrazionali e il continuo.

---

Figura 1.5: Costruzione della diagonale di un quadrato e sua proiezione sulla retta

---

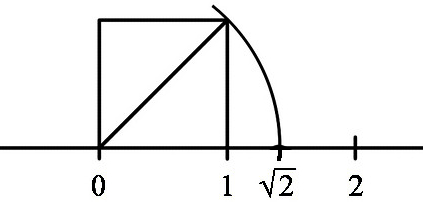
Secondo Newton e Leibniz, la continuità dei punti di una retta era dovuta alla loro densità (cioè al fatto che tra due punti se ne potesse trovare sempre un altro); ma questa proprietà valeva anche per i numeri razionali che però, non formavano un continuo (basta vedere il punto $\sqrt{2}$ della figura sopra, che sicuramente non appartiene a $\mathbb{Q}$). Dedekind si inventò così una nuova definizione; quella di sezione dell'insieme ℚ e tramite questo concetto diede una definizione dei numeri reali (compresi quelli che definirà irrazionali).
In generale una sezione di Dedekind di un insieme totalmente ordinato $\left(X,<\right)$ è una partizione di questo in due insiemi non vuoti con $\mathrm{<i>A</i>}$ t.c.

senza massimo e $\mathrm{<i>B</i>}$ t.c.

b ∈ B ⇒∀a ∈ X(b < a ⇒ a ∈ B), B taglio finale,

se il più piccolo elemento di $B$ è un razionale, allora questo corrisponderà al taglio, altrimenti, se B non ha minimo, il taglio sarà proprio un numero irrazionale (l'unico, che "riempie" il gap tra A e B). Quindi ogni taglio irrazionale corrisponde ad un numero irrazionale che non sta né in A né B, che è minore di tutti gli elementi razionali di $\mathrm{<i>B</i>}$ e maggiore di tutti gli elementi razionali di $\mathrm{<i>A</i>}$ quindi preso un segmento c’è uno ed un solo punto che determina una divisione come sopra, questo punto sarà univocamente determinato dalla coppia $\left(\mathrm{<i>A</i>},\mathrm{<i>B</i>}\right)$ e, ogni volta che in tale coppia B non ha minimo, questo punto verrà detto irrazionale.
Questa nozione è quella che definisce anche la continuità, senza più dover far ricorso al concetto di densità.

Torniamo all’infinito attuale; la definizione di infinito che si usa oggi e molti dei concetti legati ad esso si devono in larga misura a Cantor.

Definizione 1.5. Dati due insiemi $M,N$ si dice che questi sono equipotenti (o hanno la stessa cardinalità)se e solo se posso mettere in corrispondenza $M,N$ in modo tale che ad ogni elemento di un insieme ne corrisponda uno ed uno soltanto dell’altro. (corrispondenza biunivoca)

Cantor per primo, applicò questo concetto di cardinalità anche a insiemi infiniti; infatti fino ad allora, forse come retaggio della mentalità greca, si pensava che contare o confrontare non potesse essere fatto quando si trattava di infinito, e che in tal caso questo avrebbe portato a dei paradossi (si pensi a come conclude il suo discorso Galilei).
A Cantor si devono soprattutto due intuizioni che hanno la loro base nella scoperta che nell’infinito si possono fare distinzioni: la prima è che ci sono insiemi infiniti che sono equipotenti ad un loro sottoinsieme proprio, mentre la seconda è che non tutti gli insiemi infiniti possono essere messi in corrispondenza biunivoca tra di loro.
Da queste idee nascerà la definizione di infinito data da Dedekind, rovesciando completamente il modo di vedere l’infinito; si passa dall’infinito come negazione del finito, al finito come "non infinito":

Definizione 1.6 ( insieme infinito ). $$ Un insieme è infinito quando lo si può mettere in corrispondenza biunivoca (cioè se è equipotente) con un suo sottoinsieme proprio; viceversa l’insieme si dirà finito.