1.3 Rettiﬁcazione del cerchio

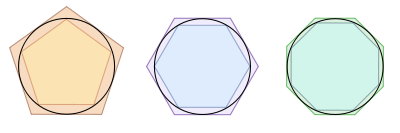
Questo problema classico in geometria consiste nel voler calcolare l'area del cerchio. La prima risoluzione del tutto corretta e rigorosamente dimostrata è quella basata sul metodo di esaustione (concetto non molto lontano da quello intuitivo di integrale di Riemann, visto come area sottesa al grafico di una funzione) ovvero:

Il metodo di esaustione permette di calcolare aree di certe figure geometriche approssimandole con una successione di poligoni che convergono alla figura data; in termini moderni diremmo che l'area cercata è il limite delle aree dei poligoni per n (=numero di lati)→ ∞.

Questo concetto anche basato sul fondamentale lemma di Eudosso, che sarà utilizzato nel calcolo della misura della circonferenza, e in molte altre applicazioni (ad esempio da Archimede).

Teorema 1.3.1 (Lemma di Eudosso). Date due grandezze (non nulle) in un certo rapporto, allora è sempre possibile trovare un multiplo di una che superi l’altra.

Figura 1.3: Il metodo di esaustione

Ovviamente l'idea di inscrivere/circoscrivere nella circonferenza poligoni ed aumentarne sempre più il numero di lati era già presente da tempo, ma ci si chiedeva se, alla fine, sarebbe stato possibile identificare i lati infinitesimi di un "ultimo poligono" con archi di circonferenza. Aristotele non era di questo avviso, infatti, sfruttando il suo concetto di infinito potenziale, sosteneva che dato un poligono con n lati era sempre possibile trovarne uno con n+1 lati che meglio avrebbe approssimato la circonferenza; la soluzione di questo problema si trova nell'uso del metodo di esaustione (attribuito ad Eudosso ed usato sia da Euclide che da Archimede), con il quale si potranno formulare importanti teoremi per il calcolo delle aree e dei volumi di molte figure. Qui vedremo come si può calcolare l'area del cerchio senza prendere in causa il concetto di infinito, e come approssimando la misura della circonferenza, che vale 2πr, si può trovare un'approssimazione di π.