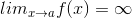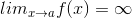
1.6 Inﬁniti e Inﬁnitesimi del calcolo diﬀerenziale

Il concetto di infinito potenziale tornò ad assumere un ruolo principale nel calcolo differenziale di Newton e Leibniz; questi, utilizzando una scrittura particolare per distinguere infiniti e infinitesimi (o flussioni come li chiamava Newton) (il simbolo ∞ per l'infinito (potenziale) ed il simbolo dt per l'infinitesimo), daranno il via ad un ramo della matematica, che è, ad oggi, uno dei più famosi: il calcolo infinitesimale dell'analisi matematica.
Oggi questi due matematici sono ritenuti i padri di questa disciplina, ma, ai loro tempi, questi non erano molto ben disposti a dividersi il merito; infatti sono passate alla storia numerose dispute tra i due riguardo a chi per primo avesse davvero scoperto il calcolo infinitesimale; attualmente si preferisce nominarli assieme, poichè hanno entrambi ottenuto risultati sorprendenti seppur lavorando separatamente.

Questa disputa nasce dal fatto che l'atto di nascita del calcolo infinitesimale è considerato il lavoro di Leibniz: "Nuovo metodo per trovare i massimi e minimi, e anche le tangenti, non ostacolato da quantità frazionarie e irrazionali e un unico genere di calcolo per quei problemi" pubblicato nel 1684 negli Acta Eruditorum; Newton però aveva raggiunto simili risultati già dal 1669, nonostante li avesse pubblicati col nome di "De Analysi per Aequationes Numero Terminorum Infinitas" solo successivamente all'opera di Leibniz nel 1711.

Dopo le scoperte di Cavalieri, Cartesio, Fermat, negli anni a cavallo tra il 1700 Newton e Leibniz formalizzarono questi concetti: a Newton si deve soprattutto l'aver introdotto: regola della catena, serie di Taylor e funzioni analitiche applicate a fondamentali problemi della fisica, mentre si devono a Leibniz la gran parte delle nozioni usate ad oggi nel calcolo infinitesimale.

Quando vennero pubblicati, questi risultati non accolsero il favore della critica, si contestava infatti la certezza dei presupposti su cui questi risultati si basavano: solo successivamente grazie ad una revisione dei risultati fatta da Cauchy, e grazie ai contributi dati da matematici come d'Alembert, Poisson, Liouville, Fourier e infine Riemann, il calcolo infinitesimale, che già era divenuto una parte fondamentale della matematica, acquistò delle besi rigorose, liberandosi di criteri non ben definiti come le "quantità infinitesime", e basandosi soprattutto sulla nozione di limite. Questa fa un uso solo potenziale dell'infinito: dire che

significa solo che il valore di f(x) supera qualsiasi quantità fissata M purchè si prenda x abbastanza vicino ad a.

Il calcolo infinitesimale fu importante non solo per la matematica; infatti molti rami della scienza e della tecnologia usano quanto appena descritto come strumento fondamentale nelle loro "descrizioni del mondo".

Analizziamo ora più approfonditamente alcuni dei problemi principali che furono studiati e/o risolti grazie a questi nuovi strumenti, mostrando le maggiori scoperte effettuate dai due protagonisti di questa sezione: Newton e Leibniz
In questo secolo, il legame tra matematica e scienza era molto stretto; infatti i principali quesiti irrisolti riguardavano argomenti di tipo "geometrico" che presentavano applicazioni pratiche: l'identificazione tra curve ed equazioni e quindi trovare la tangente ad una curva e risolvere problemi di massimo e minimo.

Si dovette aspettare l'800 per avere una base rigorosa su cui poter affrontare questi argomenti; il merito fu principalmente di Cauchy (ed anche di Weierstrass), che introdusse il concetto di limite (quello in uso ad oggi) con le notazione di ε e δ ; Cauchy soprattutto riconfermò l'uso dell'infinito potenziale, in un campo così importante della matematica.
L'unico, o comunque, uno dei più importanti problemi non ancora risolto era quello di dare una definizione rigorosa dei numeri reali; fino ad allora infatti i numeri reali erano stati usati in modo piuttosto libero, cioè senza preoccuparsi di darne una vera definizione rigorosa; sarà proprio questo il punto di partenza per lo studio dei problemi legati all'infinito moderno.