1.2.2 Paradosso della dicotomia

Questo paradosso, noto anche come paradosso dello stadio, ci permette di avvicinarci sempre di più al concetto di serie; esso aﬀerma che:
“non si può giungere all’estremità di uno stadio senza prima averne raggiunto la metà, ma poi si dovrà raggiungere la metà della metà rimanente e così via senza quindi mai riuscire ad arrivare alla ﬁne”
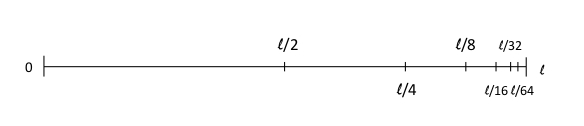
Confutare questo paradosso è molto più facile che nel caso precedente, infatti consideriamo la seguente immagine:

Figura 1.2: Il paradosso della dicotomia

essa mostra come il percorso totale che il nostro atleta dovrà compiere può essere espresso come

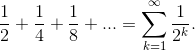
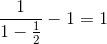Questa è una serie geometrica di ragione ½ che, come vedremo in seguito,converge a

e questo spiega perchè il nostro atleta arriverà tranquillamente alla ﬁne dello stadio.
Vediamo quindi che il “semplice” concetto di serie geometrica convergente smonta completamente la vecchia concezione che la somma di inﬁniti numeri non nulli sia necessariamente inﬁnita.