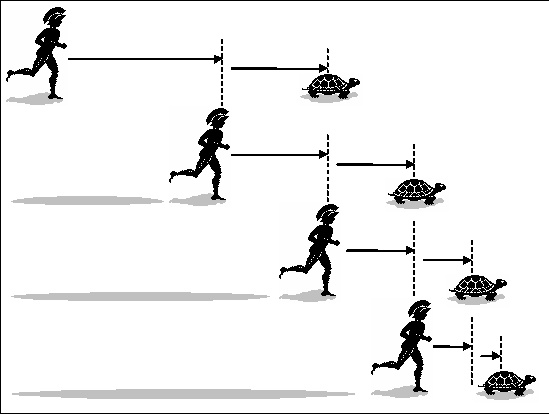
Ci occuperemo di due tra i più famosi paradossi di Zenone: tra quelli sul moto, discuteremo il paradosso di Achille e la tartaruga e quello della dicotomia.
Possiamo enunciare il paradosso come segue:
“In una corsa, il corridore più veloce non potrà mai superare quello più
lento a cui avrà dato un certo vantaggio”
ovviamente nel nostro caso si parla del corridore più veloce che è Achille
e di quello più lento che è la tartaruga.

Ragionando un po’ come Zenone e ricordando che nell’antica Grecia si pensava che la somma di infinite grandezze non nulle fosse infinita, potremmo descrivere il paradosso in questi termini: Achille dovrà percorrere in un certo tempo lo spazio che lo separa dalla tartaruga ma questa, nello stesso tempo, avrà percorso uno spazio, seppur piccolo; di nuovo Achille in un tempo successivo percorrerà questo spazio ma, nel frattempo, la tartaruga si sarà spostata ancora leggermente più avanti e così, iterando il procedimento, ne sorge il paradosso dato dal fatto che Achille dovrebbe percorrere infiniti intervalli non nulli per raggiungere la tartaruga. Diamo una dimostrazione “matematica” che ci permetterà di confutare questo paradosso.
Dimostrazione: