L’inﬁnito in crittograﬁa

Sin da tempi molto antichi si è sentita la necessità di poter comunicare in modo segreto, cioè in modo che terze parti, diﬀerenti da emissario e ricevente del messaggio, non potessero in alcun modo capire il testo del messaggio.
Il campo di studi che si occupa di quanto sopra è la crittograﬁa; facciamo alcune premesse necessarie per un uso chiaro di alcuni termini. Si parlerà di testo in chiaro per il messaggio da inviare, di testo cifrato per il messaggio cifrato, e di chiave (ciò che permette al messaggio di essere segreto).

Deﬁnizione 3.1 ( crittosistema). Data la quintupla (P, C, K, E, D) questa deﬁnisce un crittosistema se:
- $P$ è l’insieme ﬁnito dei possibili testi in chiaro
- $C$ è l’insieme ﬁnito dei possibili testi cifrati
- $K$ è l’insieme delle chiavi
- $\forall k \in$ K $\exists$ $f_{k}$ $\in E$ ed $\exists$ $g_{k}$ $\in D$ t.c. $f_{k} : P \to C,$ $g_{k} : C \to P$ sono t.c. $g_{k} (f_{k} (x)) = x$ $\forall$ $x$ $\in P$ ; $f_{k}$ sarà detta funzione di cifratura e $g_{k}$ funzione di decifrazione.

Figura 3.1: Schema di un crittosistema

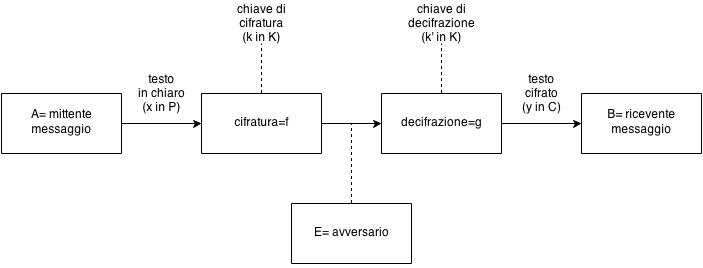
Chiaramente la funzione $f_{k}$ deve essere iniettiva (infatti esiste la funzione inversa $g_{k}$ altrimenti non si potrebbe avere l’unicità nella decifrazione; si vedrà poi nei cifrari aﬃni come questa proprietà sarà di notevole importanza. L’immagine di Figura 3.1 rappresenta lo schema classico di un crittosistema (si ricordi che nella crittograﬁa moderna si assume sempre che l’intercettatore conosca l’algoritmo usato per cifrare/decifrare).
In questo capitolo ci occuperemo di cifrari a chiave simmetrica: ovvero cifrari (e cioè uno strumento crittograﬁco che cifra ogni stringa di caratteri) la cui chiave è conosciuta da mittente e ricevente. La sicurezza di questi sistemi è basata principalmente sulla diﬃcoltà per terze parti di trovare la chiave; si deﬁnisce attacco a forza bruta quello consistente nel provare tutte le chiavi possibili. Ovviamente questa è l’ultima risorsa a cui si deve fare ricorso e spesso questi tentativi richiederebbero un tempo superiore alla stessa età dell’universo !! Si fa perciò ricorso ad altri metodi, come l’analisi di frequenza.
Esiste un sistema indecifrabile che ha, ovviamente, un costo altissimo, ed è un crittosistema sviluppato in prima sede da Vernam e successivamente da Mauborgne; sarà di questo sistema che ci occuperemo con un particolare interesse al ruolo che l’inﬁnito ha avuto nel garantire a questo crittosistema il primato di inviolabilità.