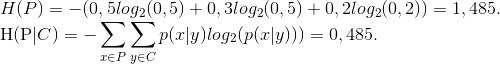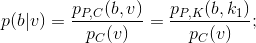
Mostriamo ora che OTP ha sicurezza perfetta (o assoluta); per fare questo ci poniamo alcune domande: dati come al solito P,C,K (con la scelta di K indipendente dalla scelta di P), ci chiediamo quanto vale H(K|C) e soprattutto se H(K|C) < H(K).

Definizione 3.7 ( crittosistema a segretezza assoluta). Un crittosistema si dice avere sicurezza perfetta se H(P|C) = H(P)

Facciamo un esempio in cui questo non accade:

Esempio:
Siano P = a,b,c   C = u,v,w   K = k1,k2   con:

p(a) = 0, 5,   p(b) = 0, 3,   p(c) = 0, 2

p(k1) = p(k2) = 0, 5   e   P,K   indipendenti

Sia poi ek la funzione di cifratura rispetto alla chiave k t.c.:

e(k1)(a)=u,   e(k1)(b)=v,   e(k1)(c)=w

e(k2)(a)=u,   e(k2)(b)=w,   e(k2)(c)=v
Posta pC(u)=probabilità che il testo cifrato sia u:

pC(u)= p(k1)p(a)+p(k2)p(a)=(0,5)(0,5)+(0,5)(0,5)=0,5

Analogamente pC(v) = 0, 25,   pC(w) = 0, 25
Calcoliamo ora p(b|v)ricordando la definizione:

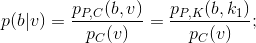
poichè abbiamo assunto che P e K fossero indipendenti

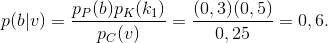
Analogamente

p(a|w) = p(a|v) = 0;   p(b|v) = p(c|w) = p(c|w) = 0, 4;   p(b|w) = 0, 6.

Possiamo quindi ora calcolare le entropie che ci interessano ricordando le definizioni.

Pagina precedente Pagina precedente