Deﬁnizione 3.5 (entropia congiunta)

cioè l’entropia relativa all’incertezza della variabile Z = (X,Y)

Deﬁnizione 3.6 (entropia condizionata)

cioè l’entropia relativa all’incertezza di Y una volta noto il valore assunto da X.

Questa deﬁnizione è di immediata deduzione infatti:

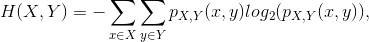
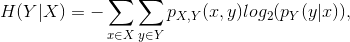
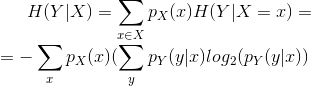
per la deﬁnizione di probabilità condizionata

Teorema 3.2.3 (regola della catena)

H(X,Y) = H(X) + H(Y|X)
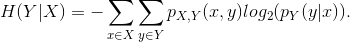
cioè l'incertezza dell'evento congiunto è data dall'incertezza su X sommata all'incertezza su Y noto il valore assunto da X.

Dimostrazione:

Proposizione 3.2.4. Valgono le seguenti tre proprietà di H:
(1)

H (X) \leq l o g_{2} (n) dove n è il numero dei possibili esiti di x;
vale l’uguaglianza se tutti gli esiti possibili sono equiprobabili (questo signiﬁca
che la massima entropia si ha per distribuzione di probabilità uniforme) (2) H (X, Y) \leq H (X) + H (Y) e        vale        l’uguaglianza        solo        nel        caso        in        cui X, Y siano indipendenti (3) H (Y | X) \leq H (Y) e vale l’uguaglianza solo nel caso in cui X, Y siano indipendenti (questo signiﬁca che il condizionamento riduce l’entropia,
cioè X può dare solo informazioni su Y,
non accrescere la sua incertezza)Il risultato (3), nonchè il più importante, discende dalla regola della catena e
dal punto (2), infatti:H (X) + H (Y | X) = H (X, Y) \leq H (X) + H (Y) .