Teorema 3.2.5. Dato un crittosistema con n chiavi equiprobabili con probabilità
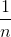e t.c. per ogni ,
c’è una ed una sola chiave k t.c. ;
allora questo sistema ha sicurezza perfetta.
Perciò nel precedente esempio, conoscere il testo cifrato riduce notevolmente l’incertezza del testo in chiaro. Proviamo che per OTP questo non succede.
Dimostrazione:Questo risultato permette in realtà di enunciare un teorema più generale
Teorema 3.2.5. Dato un crittosistema con n chiavi equiprobabili con probabilità
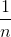e t.c. per ogni ,
c’è una ed una sola chiave k t.c. ;
allora questo sistema ha sicurezza perfetta.
Ad esempio, uno dei cifrari più usati attualmente, l'RSA (algoritmo a crittografia a chiave pubblica), non è un cifrario a sicurezza assoluta; infatti disponendo di
tempo sufficiente posso decifrare tutti i testi cifrati possibili fino a trovare
p.
L’entropia ovviamente non tiene in considerazione il tempo di calcolo, ma RSA
proprio per la complessità computazionale della fattorizzazione è comunque
ritenuto sicuro.
In conclusione abbiamo mostrato come grazie all’introduzione di una chiave
teoricamente infinita e irripetibile, il cifrario di Vernam sia l’unico, anche a fronte
di cifrari più moderni come RSA, ad avere sicurezza assoluta; cioè anche in
crittografia l’infinito ha un ruolo centrale e insostituibile.
