Nel 1917 Gilbert S. Vernam era un giovane ingegnere che lavorava alla American Telephone & Telegraph Company (AT&T) nella sezione dedicata alla telegraﬁa a stampa diretta; il problema di cui si stava occupando allora era quello della sicurezza di questo metodo.
L’idea di Vernam era quella di basare la protezione su un sistema crittograﬁco la cui principale caratteristica era quella di ”combinare” testo in chiaro e chiave.
Possiamo vedere questo metodo in due modi diversi ma tra loro equivalenti; il primo e il più semplice è quello di vedere il metodo di Vernam come un procedimento che somma la frase da criptare alla chiave (associando come al solito ad ogni lettera il corrispondente numero secondo lo schema: a=0, b=1...).
Il secondo modo di vedere il metodo è quello di sfruttare l’operatore logico XOR; ogni carattere del testo in chiaro viene rappresentato mediante 5 unità (che sono tradizionalmente 0 o 1, cioè la presenza o l’assenza di un impulso elettrico), quindi in totale si hanno

2^{5} = 32

diverse combinazioni che corrispondono alle lettere dell’alfabeto e ad altri simboli di punteggiatura.
Una volta fatto questo e interpretata anche la chiave in questo modo, si sommano le due sequenze di 0, 1 ottenute secondo le regole del codice binario (senza riporti) ovvero:
-1+1=0
-0+0=0
-1+0=0+1=1
Facciamo un esempio in entrambi i modi:

Esempio:
(primo modo) supponiamo di volerecriptare il messaggio "hello", allora procederemo come segure (i calcoli sono fatti tutti mod 26):

testo in chiaro	h	e	l	l	o
testo in chiaro (numerico)	7	4	11	11	14
chiave	x	m	c	k	l
chiave (numerica)	23	12	2	10	11
testo cfrato (numerico)(somma)	30	16	13	21	25
testo cifrato	e	q	n	v	z

Tabella 3.2: Primo metodo di cifratura

(secondo modo) supponiamo di voler criptare la lettera a (a=11000), allora procederemo come segue:

testo in chiaro	1	1	0	0
chiave	1	0	1	1
testo cfrato (somma binaria)	0	1	1	1

Tabella 3.2: Secondo metodo di cifratura

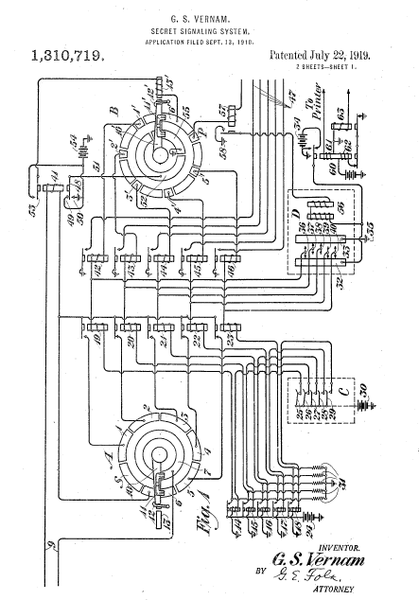
La realizzazione ingegneristica di questo cifrario è basata sulla tecnica del nastro di carta perforato; una macchina, in grado di leggere due nastri perforati in entrata (chiave e testo in chiaro) combinarli nel modo scritto sopra e dare in uscita il nastro perforato del corrispondente testo criptato; viceversa ma sempre con la stessa macchina, dando in input testo da decifrare e chiave, ne usciva in output il testo in chiaro.

Si deve a Vernam anche l’aver completamente automatizzato, e quindi eliminato l’intervento umano, in questa catena di comunicazione; questo quindi è un primo passo verso la moderna e completa tecnologizzazione di tutto il processo.
Invertendo il procedimento, per decriptare un codice basta sottrarre al testo cifrato la chiave, ragionando come sopra.
Nei primi tempi le chiavi avevano la forma di un ciclo di nastro di carta perforato con sequenze di 0,1 casuali; quindi ogni chiave passava attraverso la macchina ad intervalli regolari, permettendo facilmente a terze parti di trovare la chiave con l’analisi delle frequenze del metodo Kasiski.
Si provò a risolvere questo problema allungando di molto la chiave, ma ovviamente questa diventava allora molto diﬃcile da maneggiare nelle macchine; si deve però a J. O. Mauborgne (un uﬃciale dell’esercito) la risoluzione di questo problema.
Egli capì che per evitare questi problemi la chiave doveva essere inﬁnita, senza senso e completamente casuale (random), e da qui viene il nome OTP.
Ecco che interviene ﬁnalmente l’inﬁnito; il suo ruolo non solo è centrale per permettere alla macchina di essere completamente eﬃciente ma anche perchè, come dimostrerà Shannon, grazie alle ipotesi di cui sopra, questo sistema è completamente sicuro in teoria ed in pratica, ed è anche il solo ad esserlo.

3.2 Cifrario di Vernam