Definizione 3.3 (probablità condizionata).
Si definisce la probabilità condizionata di y rispetto a x (cioè la probabilità di
sapendo che vale )
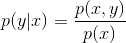
Definizione 3.4 (variabili indipendenti). Date variabili aleatorie, si dice che queste sono indipendenti se p(y|x)=p(y), cioè se la probabilità di y non varia sapendo quanto vale x.
Teorema 3.2.1 (Teorema di Bayes).
Siano X,Y variabili aleatorie, allora vale che
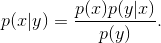
Un concetto molto importante per le sue applicazioni alla teoria dell’informazione
è quello di Entropia; intuitivamente si può definire l’Entropia come la
misura dell’incertezza di un certo risultato, ma diamone una definizione
rigorosa.
Consideriamo le seguenti condizioni che deve soddisfare la
misura dell’incertezza di un risultato che denotiamo con
:
(1)
deve essere continua e funzione della distribuzione delle probabilità;
(2)
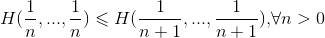
cioè la misura dell’incertezza deve crescere al crescere del numero dei possibili esiti equiprobabili;
(3) vale che
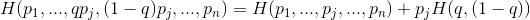
cioè se un esito presenta due possibili casi allora la misura
dell’incertezza aumenta ed è data dall’incertezza del valore pj e da
quella causata dalla presenza dei due casi.
Uno dei maggiori esponenti della crittografia classica, Claude Shannon, formulò
il seguente teorema:
Teorema 3.2.2.
Sia
una funzione che soddisfi le proprietà di cui sopra, allora
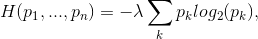
e H(x), con =costante positiva.
Quindi ne segue che possiamo assumere come misura dell’incertezza dell’esito
di :
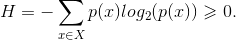
Un’altra interpretazione dell’entropia vede questa grandezza come il numero di domande vero/falso da porre per conoscere l’esito di un esperimento; di conseguenza in crittografia si può immaginare che l’entropia rappresenti la difficoltà di ricavare informazioni contenute in messaggi che occorre decifrare, si può pensare ad esempio a come ottenere una chiave.