Consideriamo quindi un cifrario OTP con alfabeto
${\mathbb{Z}}_{\mathrm{₂}}=\left\{0,1\right\},P=C=K=$ {0,1}${}^{\mathrm{^l}}$ dove $l$ è un intero che mi dà la lunghezza di $P,C,K$ ed assumiamo che le chiavi siano casuali e quindi tutte con uguale probabilità cioè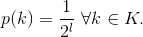
Dato allora il testo cifrato $c\in C$ e ricordando che $P,K$ sono indipendenti,

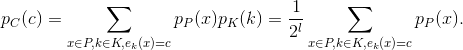
Poichè ad ogni messaggio in chiaro e messaggio cifrato corrisponde una sola chiave t.c. e_k(x)=c,ogni x compare nella sommatoria una sola volta e quindi basta ridurre l’indice della sommatoria a x ∈Pe ricordare che la somma delle probabilità di tutti i possibili testi in chiaro è 1, cioè:

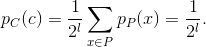
Questo mi dice semplicemente che tutti i testi cifrati sono equiprobabili; passiamo ora al calcolo delle entropie.
Per quanto appena visto tutte le $2^{\mathrm{^l}}$ possibilità per sono equiprobabili e quindi

H(K) = H(C) = log ₂ (2^l) = l

Calcoliamo ora $H\left(P,K,C\right)$ in due modi differenti:
poichè $\mathrm{<i>C</i>}$ è univocamente determinato da :

H(P,K,C) = H(P,K)

poichè sono indipendentiH(P,K,C) = H(P) + H(K)

e inoltre vale anche che H(P,K,C) = H(P,C) = H(P|C) + H(C)
Uguagliando ora i due termini e ricordando che $H\left(K\right)=H\left(C\right)$ ne verrà che

H(P) = H(P|C)
e questo per definizione prova che il sistema ha sicurezza perfetta. □