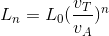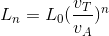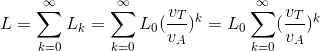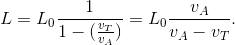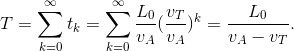Indichiamo rispettivamente con i pedici A, T le grandezze riferite ad Achille e alla tartaruga, con Li la lunghezza del tratto i-esimo percorso dalla tartaruga e con ti i tempi i-esimi impiegati da Achille per percorrere questi tratti; supponiamo vA>vT, ora:
in tale tempo la tartaruga percorrerà uno spazio
e Achille percorrerà questa distanza in un tempo pari a
Quindi iterando il procedimento, al passo n-esimo avrò che:
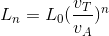

Considerando allora le rispettive serie e passando al limite, avrò che:
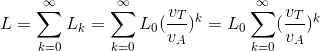
poichè abbiamo una serie geometrica di ragione <1 per ipotesi, avremo che è essa convergente e vale:
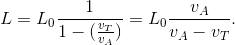
Infine
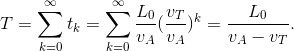
per gli stessi ragionamenti fatti sopra.
Ma allora il tempo T impiegato da Achille per raggiungere la tartaruga è un tempo finito, cioè questa dimostrazione che utilizza le serie, "smonta" il paradosso di Achille e la tartaruga.
□