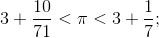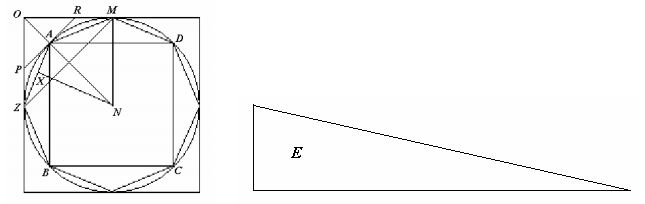
Teorema 1.3.2. L’area del cerchio (A) è uguale all’area del triangolo avente per base la circonferenza e per altezza il raggio.

Dimostrazione:

Figura 1.4: Costruzione del poligono inscritto

Nella raccolta dei lavori di Archimede, dopo questa proposizione si trova la prima approssimazione che Archimede ha dato del numero π:

questa approssimazione è stata data grazie alla proposizione seguente:

Proposizione 1.3.3. Se un angolo di un triangolo è diviso dalla bisettrice congiungente il lato opposto, allora i segmenti di questo lato sono nello stesso rapporto con i restanti lati del triangolo; e, se i segmenti della base sono nello stesso rapporto con i restanti lati del triangolo, allora la linea retta che congiunge il vertice al punto di separazione sarà la bisettrice dell’angolo del triangolo.

Nonostante questo valore sia molto preciso, Archimede non aveva i mezzi per dimostrare che π non si può scrivere come frazione; successivamente è stato provato che π è un numero irrazionale (la dimostrazione di ciò è del 1761) e per di più trascendente (dimostrato nel 1882).
Quindi riassumendo possiamo dire che il concetto di infinito dei greci fu ben presto messo in discussione soprattutto dal fatto che la somma di infiniti numeri potesse non essere infinita; è proprio su questo ultimo argomento che si basa il concetto di serie.