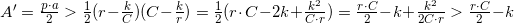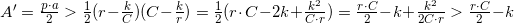Supponiamo per assurdo che i due non siano equivalenti, allora o il cerchio ha area maggiore rispetto al triangolo, o minore.
(1) Supponiamo per assurdo che il cerchio abbia area minore del triangolo; supponiamo cioè che $ k>0 t.c.
inscriviamo poi nel cerchio un poligono regolare t.c. il suo apotema a sia:
e il suo perimetro p sia:
Questo lo posso sempre fare poichè basta considerare un poligono con un numero alto di lati affinchè a sia vicino a r e p sia vicino a C.
Quindi l'area A' del poligono è
ma allora:
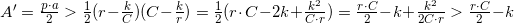di conseguenza:
Ma questo è un assurdo poichè avevamo supposto che
ne verrà che l'area del cerchio non può avere area minore del triangolo.
(2) Analogamente, per la disuguaglianza inversa, si procede supponendo per assurdo che il cerchio abbia area maggiore, e considerando poligoni circoscritti.
Ma allora questo prova che area del cerchio e area del triangolo costruito come da ipotesi sono uguali.
□
