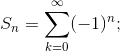
Analizziamo più attentamente la serie di Grandi:

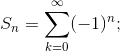
abbiamo già visto che non converge (nel senso di cui sopra, mentre si ha convergenza secondo Cesaro a ½ ) ma facciamo vedere come questa serie sia stata, nel corso dei secoli, oggetto di grandi discussioni.
(1) si potrebbe pensare di procedere in questo modo:

$S_{n} = 1 - 1 + 1 - 1 + 1 - 1 + . . . = 1 - (1 - 1 + 1 - 1 + . . .) = 1 - S_{n}$

e ne verrebbe che S_n= ½
(2) alternativamente potremmo pensare: $S_{n}$ =(1-1)+(1-1)+...=0
(3) o ancora: $S_{n}$ =1+(-1+1)+(-1+1)+...=1

Questi esempi sono molto importanti perchè mostrano come per le serie non valgano le classiche proprietà (come l’associatività e la commutatività della addizione) che valgono per le somme finite.
Proprio su questa serie è basato il paradosso della lampada di Thomson:

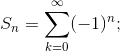
”si consideri una lampada accesa con un tasto di accensione e si consideri il seguente procedimento: dopo un minuto si spenga la lampada, dopo mezzo minuto la si accenda di nuovo e si ripeta il procedimento dimezzando sempre i tempi. Dopo due minuti la lampada sarà accesa o spenta ? “
Possiamo interpretare questo paradosso tramite la serie di Grandi

e cioè se ne può dedurre che in realtà questo paradosso non ha una risposta perchè la nostra serie è oscillante e quindi nulla si può dire sul risultato.

Fino ad ora abbiamo quindi smontato l'idea dell’inﬁnito greca in 3 modi diﬀerenti; abbiamo fatto vedere che somma di inﬁniti numeri può benissimo dare inﬁnito ma può anche dare un numero ﬁnito oppure può non essere determinata (si veda la proposizione di cui sopra); quindi l’idea di una distinzione netta tra inﬁnito in potenza e in atto sembra non essere più molto sicura. Vediamo come si svilupperà il concetto di inﬁnito in anni succcessivi.