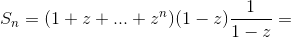

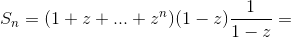

- :
Quindi per =1
se considero il
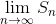 questo vale ∞ e cioè la serie diverge per z=1
questo vale ∞ e cioè la serie diverge per z=1
Per z ≠ 1 invece Sn
è convergente ⇔
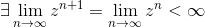 ;
distinguiamo quindi 3 casi al variare di :
;
distinguiamo quindi 3 casi al variare di :
(1) |z|<|zn| 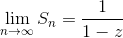
(2)|z|>1|zn|
(3) |z|=1
e z ≠ 1
supponiamo per assurdo che ∃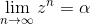 ma allora
ma allora 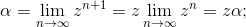 ; cioè α=zα
; cioè α=zα
Quindi le ipotesi sono 2: o z=1 e questo è assurdo per ipotesi, oppure α=0, ma se vale questo allora
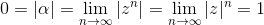 per quanto visto all’inizio, e questo è assurdo.
per quanto visto all’inizio, e questo è assurdo.
Quindi in questo caso la serie non converge. □