Definizione 2.3. $\forall \alpha \in ℝ,\alpha \ge 0$ definiamo

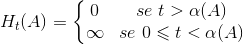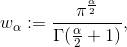
dove $\Gamma$ è la funzione gamma di Eulero definita per $s>0$:

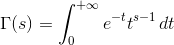
Si può osservare che w_α è una costante dimensionale che dipende solo da α e nel caso in cui α sia un numero intero positivo: w_α = misura di Lebesgue $\alpha$ dimensionale del disco unitario.

Definizione 2.4. Per ogni $A\subseteq {ℝ}^{\mathrm{ⁿ}}$, $A$ non vuoto, definiamo:
1)

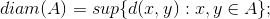
2)

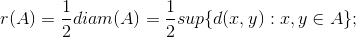
(dove con $d\left(x,y\right)$ intendiamo la distanza euclidea tra $x$ e $y$)

3)

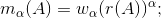
$\forall \alpha$ reale positivo

4) se $A=\varnothing$ definiamo $m_{\mathrm{_\alpha}}\left(A\right)=0$

Per ogni A⊆ℝⁿ fissato δ reale positivo, si chiama δ ricoprimento di A una famiglia 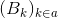di sottoinsiemi di ℝⁿ t.c.:
i) a sia finito o numerabile
ii) diam(B_k)≤δ ∀ k ∈a
iii)

Definiamo inoltre:

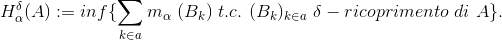
Vale che se 0$<{\delta }^{\prime }<\delta$, ogni ${\delta }^{\prime }$-ricoprimento di $\mathrm{<i>A</i>}$ è anche un $\delta$-ricoprimento di $\mathrm{<i>A</i>}$ e quindi 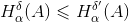, cioè se consideriamo la funzione

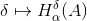
questa sarà monotona decrescente e di conseguenza avrà limite per $\delta \mapsto 0^{+}$.

Definizione 2.5. Si chiama allora misura di Hausdorff $\alpha$-dimensionale:

Proposizione 2.0.4. H_αè una misura metrica rispetto alla distanza euclidea, cioè, valgono le seguenti proprietà:

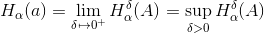
1) H_α(∅) = 0

2)H_α(A) ≤ H_α(B)   con   A ⊆ B
3)H_α   è subadditiva
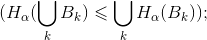
4)
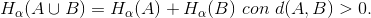
Definizione 2.6. Si dice che $A\subseteq {ℝ}^{\mathrm{ⁿ}}$ è un insieme $H_{\mathrm{_\alpha}}$ misurabile se per ogni $E$ sottoinsieme di ${ℝ}^{\mathrm{ⁿ}}$ vale che: H_α(E)=H_α(E∩A)+H_α(E∩A^C)