2.0.3 Frattali famosi

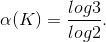
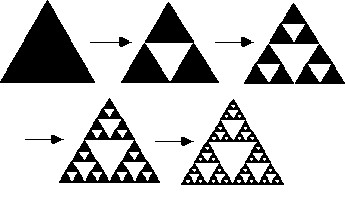
Un altro frattale molto famoso è il triangolo di Sierpinski $S$ ; si può vedere che ha misura di Lebesgue (mis) (in questo caso corrisponde all’area del triangolo) pari a 0, mentre:

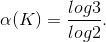
Si considera un triangolo equilatero “pieno”, poi lo si divide in 4 triangoli equilateri unendo i punti medi dei lati,e si toglie quello centrale, si ripete inﬁne questo ultimo passaggio su ognuno dei trangoli ottenuti e si itera il procedimento, ottenendo:

Figura 2.5: Triangolo di Sierpinski

Gli esempi appena visti sono frattali lineari, è cioè frattali il cui algoritmo generatore è lineare; oltre a questi però abbiamo anche frattali non lineari (in cui l’algoritmo generatore presenta equazioni di ordine superiore a 1) e frattali aleatori (che, come dice il nome, derivano la loro forma da quantità scelte a caso).
Da frattali, relativamente semplici come quelli visti sopra, oggi si studiano frattali come quelli di Mandelbrot o quelli di Julia, estremamente complessi.
Questo uso dell’inﬁnito come inﬁnitamente ripetuto non ha aﬀascinato solo i matematici ma ha contagiato molti campi del sapere, infatti esistono numerose opere artistiche, letterarie o musicali ispirate proprio alla geometria frattale; come detto nell’introduzione, il concetto di inﬁnito non appartiene solo ai matematici.

Figura 2.6: Insieme di Mandelbrot

Figura 2.7: Insieme di Julia