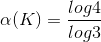
Un altro famoso esempio di frattale è la curva di Koch,
(o fiocco
di neve di Koch, o merletto di Koch); si tratta sempre di considerare l’intervallo
chiuso e
di dividerlo in 3 parti.
Nella parte centrale viene poi costruito un triangolo equilatero avente come base
la parte centrale stessa, e si ripete così questo procedimento, dividendo
ripetutamente in 3 parti ogni lato della costruzione e costruendo nel segmento in
mezzo un triangolo equilatero, che ha il segmento stesso come base (la base viene
sempre tolta dalla costruzione).
In questo caso, al contrario di quanto mostrato sopra, si ha che la misura di
Lebesgue (mis) della curva di Koch è infinita mentre
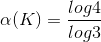
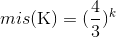ma allora al limite per k↦+∞:
mis(K)=
Per la dimostrazione di ,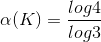
si procede analogamente a sopra; osserviamo che in questo caso, ogni segmento viene diviso in 4 parti, ognuna delle quali ha lunghezza pari a
⅓ di quella del segmento
iniziale; cioè:
e
