Coste della Bretagna:
partendo dal classico concetto di dimensione, Mandelbrot aﬀermò che la lunghezza di una costa aveva dimensione d: 1 < d < 2
Mandelbrot infatti propose il seguente metodo di misura:
ovviamente la lunghezza di un tratto di costa costa sarebbe stata più di quella del segmento che congiungeva i due estremi dato che la costa era piuttosto frastagliata, allora si poteva prendere un compasso di apertura ﬁssata e farlo avanzare lungo la costa in modo che ogni passo iniziasse dove ﬁniva il precedente.
In questo modo moltiplicando il numero dei passi per l’ampiezza del compasso si sarebbe ottenuta la lunghezza cercata. Più si riduce l’ampiezza del compasso, più la lunghezza della costa tende ad aumentare.
Ma allora si è visto che, a seconda dell’ampiezza dell’apertura del compasso, si possono ottenere sia i dettagli che il carattere generale della costa, senza però riuscire a dare una vera misura della sua lunghezza.
Poichè si può approssimare una costa al merletto di Koch e sappiamo (si vedrà successivamente) che questo ha lunghezza inﬁnita, ne verrà che anche la lunghezza della costa della Bretagna è inﬁnita.

Figura 2.2: Costa dell’Inghilterra a misurazioni sempre più precise

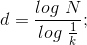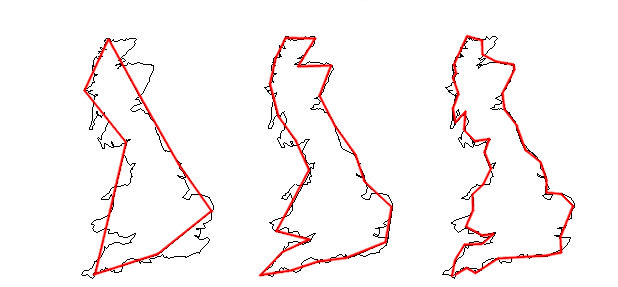
Da queste osservazioni si arrivò a deﬁnire un’altra importante proprietà dei frattali, e cioè quella di avere dimensione non intera; in particolare Mandelbrot osservò che una curva per avere dimensione compresa tra 1 e 2 deve avere superﬁcie nulla e lunghezza inﬁnita (analogamente una superficie con dimensione compresa tra 2 e 3 deve avere area infinita e volume nullo ).
La parola stessa frattale deriva da questo suo carattere caotico, frazionario, spezzato; sta infatti ad indicare la dimensione non intera.

Deﬁnizione 2.2. ( frattale) Un frattale è un oggetto matematico di dimensione frazionaria pari a

dove $N$ sono le parti simili all’oggetto intero in cui questo può essere diviso e $k$ è il rapporto di omotetia.
(Infatti per ogni frattale possiamo vedere $N$ copie autosimili, tutte ottenute mediante una omotetia di rapporto $k$ ).