
L’insieme di Cantor è il più noto sottoinsieme di
avente dimensione di Hausdorff non intera; vediamo di cosa si tratta.
Consideriamo l’intervallo chiuso
e costruiamo l’insieme di Cantor
in questo modo:

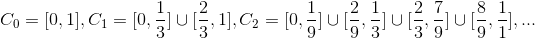
Iterando quindi il procedimento avrò che
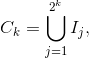
dove Ij sono intervalli di
lunghezza pari a 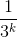 , e si definirà
quindi l’insieme di Cantor C
, e si definirà
quindi l’insieme di Cantor C
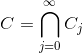
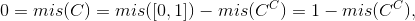
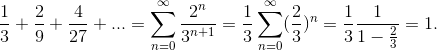
Ci rimane ora da provare che
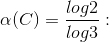
osserviamo innanzitutto che la famiglia
(Ck) definita come sopra è un δ-ricoprimento di C
con
δ=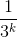 , quindi per definizione avrò che:
, quindi per definizione avrò che:
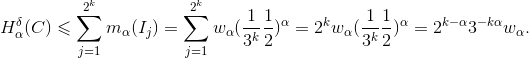
Posto ora
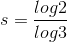 ne viene che
ne viene che
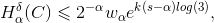
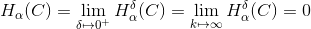
Osservando questo insieme da un punto di vista più generale, possiamo
notare che è molto evidente la proprietà di autosimilarità, infatti ogni
intervallo Ck è simile a C sono contenute tutte le informazioni necessarie per sapere
come è fatto tutto l’insieme; proprio per questo l’insieme di Cantor è uno dei
primi e più semplici esempi di frattali.
Ricordando la prima definizione di frattale, possiamo osservare che, in effetti, ad ogni
passo da un segmento inziale vengono generati 2 segmenti, di lunghezza pari a ⅓ di quella del segmento
iniziale; cioè
e
proprio come si è appena provato.