

 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

|

|
Finora abbiamo seguito questa linea; abbiamo definito le applicazioni affini tra spazi affini in modo puramente algebrico e sucessivamente abbiamo dedotto alcune proprietà di natura geometrica, in particolare per le affinità.
Vogliamo ora caratterizzare le affinità tramite proprietà di natura geometrica: essendo le affinità i veri automorfismi di uno spazio affine, capiremo senz'altro meglio quale sia la natura di questi ultimi in termini piú propriamente geometrici.
30. OSSERVAZIONE Sia
Allora
DIMOSTRAZIONE Siano
se
PARTE i
PARTE ii sia ora
Grazie a parte i sappiamo che
Terminologia:
- un'applicazione
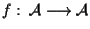 biunivoca che possiede la proprietà
biunivoca che possiede la proprietà 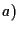 è detta quindi conservare il parallelismo e la terminologia è giustificata dall'osservazione precedente.
è detta quindi conservare il parallelismo e la terminologia è giustificata dall'osservazione precedente.
- sia
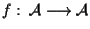 biunivoca; diciamo che
biunivoca; diciamo che 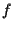 "conserva il rapporto" (di segmenti orientati paralleli) se, dati
"conserva il rapporto" (di segmenti orientati paralleli) se, dati
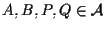 ,
,
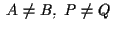 e
e
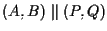 allora
allora
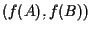 e
e
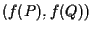 sono ancora segmenti orientati paralleli e
sono ancora segmenti orientati paralleli e
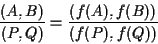

 _______________
_______________
 __
__
 ________________________
________________________