

 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

|

|
12. PROPOSIZIONE Sia
2.
13. DEFINIZIONE Sia
- se
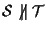 e
e 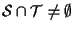 diciamo che
diciamo che 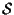 e
e 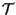 sono incidenti (non si tratta quindi di un termine sinonimo di "non disgiunti");
sono incidenti (non si tratta quindi di un termine sinonimo di "non disgiunti");
- altrimenti, se
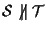 ma
ma 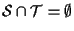 ,
diciamo che
,
diciamo che 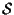 e
e 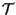 sono sghembi.
sono sghembi.
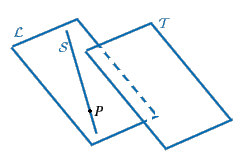
Ovviamente la posizione reciproca di due sottospazi affini
rientra in uno e una solo dei tre casi possibili: paralleli, incidenti,
sghembi (si pensi ad esempio a due rette nello spazio ordinario). 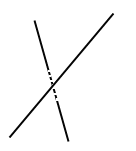
rette sghembe
14. ESERCIZI
Gli esercizi esaminano varie correlazioni particolari tra le relazioni insiemistiche "essere contenuto" o "essere disgiunti" e il parallelismo.


 _______________
_______________
 __
__
 ________________________
________________________