PARALLELISMO: DEFINIZIONE GENERALE

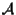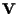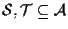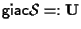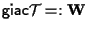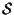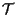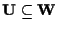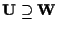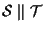10. DEFINIZIONE Sia $\mathcal{A}$ spazio affine su $\mathbf{V}$ e siano $\mathcal{S},\mathcal{T} \subseteq \mathcal{A}$ sottospazi affini; posto $\mathsf{giac}\mathcal{S}=:\mathbf{U}$ e $\mathsf{giac}\mathcal{T}=:\mathbf{W}$ diciamo che $\mathcal{S}$ è parallelo a $\mathcal{T}$ se $\mathbf{U} \subseteq\mathbf{W}$ oppure $\mathbf{U} \subseteq\mathbf{W}$ . Scriveremo ancora $\mathcal{S}\parallel\mathcal{T}$ .

Si noti che se $\mathcal{S}$ e $\mathcal{T}$ hanno la stessa dimensione allora ritroviamo la definizione 1 di parallelismo già data.

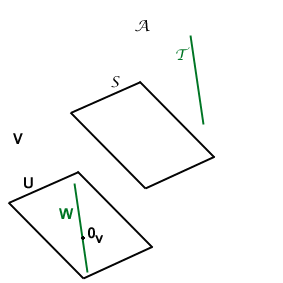
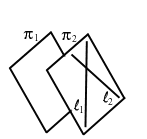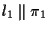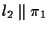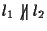Si osservi la figura a lato relativa allo spazio ordinario: certamente $l_{1}\parallel\pi_1$ e $l_{2}\parallel\pi_2$ ma $l_{1}\not\,\parallel\l _2$ ; ne deduciamo che nell'insieme di tutti i sottospazi affini di un dato spazio affine la relazione "essere paralleli" non è una relazione di equivalenza: essa è banalmente riflessiva e simmetrica ma non è piú transitiva.
In ogni modo gran parte dei risultati trovati relativamente al parallelismo tra sottospazi della stessa dimensione possono essere generalizzati con le opportune modifiche.

______

_______________

________________________