PARALLELISMO TRA SOTTOSPAZI ARBITRARI IN TERMINI DI TRASLAZIONI (2)

11. PROPOSIZIONE Sia

spazio affine su $\mathbf{V}$ e siano $\mathcal{S},\mathcal{T} \subseteq \mathcal{A}$ sottospazi affini; supponiamo che

, allora

DIMOSTRAZIONE
$\Rightarrow$ ) Sia $\mathcal{S} \parallel \mathcal{T}$ allora, posto $\mathcal{S}=\mathsf{S}(P,\mathbf{U})$ e $\mathcal{T}=\mathsf{S}(Q,\mathbf{W})$ , avremo che $\mathbf{U} \subseteq \mathbf{W}$ .
A questo punto affermiamo che, posto 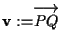$\mathbf{v}:=\stackrel{\displaystyle{\longrightarrow}}{PQ}$ , otteniamo una traslazione che fa al caso nostro: infatti esattamente come in proposizione 4 segue che

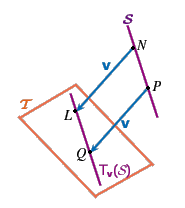
sia

cioè

; vorremmo

cioè

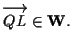
Facciamo vedere come suggerito dal disegno che

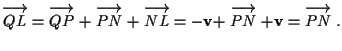
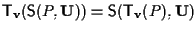$\Leftarrow$ ) Viceversa supponiamo che esista $\mathbf{v} \in \mathbf{V}$ tale che $\mathsf{T}_{\mathbf{v}}(\mathcal{S})\subseteq\mathcal{T}$ ; ora noi sappiamo che

(vedi lemma 3) e sappiamo che

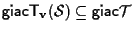(vedi esercizio 9 della sezione "Sottospazi affini") e quindi abbiamo $\mathbf{U} \subseteq \mathbf{W}$ cioè che $\mathcal{S} \parallel \mathcal{T}.$

______

_______________

________________________