DEFINIZIONE DI PARALLELISMO TRA SOTTOSPAZI DELLA STESSA DIMENSIONE

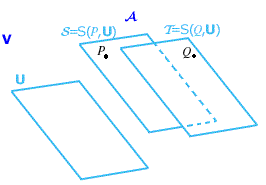
1. DEFINIZIONE Sia $\mathcal{A}$ spazio affine su $\mathbf{V}$ e siano $\mathcal{S},\mathcal{T}$ sottospazi affini di $\mathcal{A}$ aventi la stessa dimensione; diciamo che $\mathcal{S}$ e $\mathcal{T}$ sono paralleli se hanno la stessa giacitura e in tal caso scriveremo $\mathcal{S} \parallel \mathcal{T}$ (altrimenti scriveremo $\mathcal{S}\not\, \parallel \mathcal{T}$ ).

Una nozione di parallelismo piú generale sarà data altrove.

2. OSSERVAZIONE Sia $\mathcal{A}$ spazio affine su $\mathbf{V}$ ; poniamo $\mathsf{dim}\mathcal{A}=n$ e sia $d \in \mathbf{N}\;,\;0 \leq d \leq n$ ; nell'insieme $\mathcal{H}_d$ dei sottospazi di $\mathcal{A}$ di dimensione

la relazione ''essere paralleli'' è una relazione di equivalenza.

Si osservi che due punti di $\mathcal{A}$ sono sempre paralleli.

______

_______________

_________________