IL TRASLATO DI UN SOTTOSPAZIO

I disegni che facciamo relativamente al piano ordinario ci suggeriscono che due rette sono parallele se e solo se esiste una traslazione che sposta una nell'altra.

La stessa cosa accade nello spazio ordinario: si condideri a titolo esemplificativo come coppia di piani paralleli quella costituita da soffitto e pavimento

di una stanza -di un edificio non troppo post-moderno!- (e chiaramente soffitto e pavimento rappresentano solo una porzione dei piani geometrici); ancora dovrebbe essere chiara l'esistenza di una traslazione che porta l'uno sull'altro. Daremo ora l'enunciato e la dimostrazione formali di questi fatti in uno spazio affine astratto.

Premettiamo alla proposizione un lemma che ci dice cosa otteniamo quando trasliamo un sottospazio affine.

3. LEMMA Sia $\mathcal{A}$ spazio affine su $\mathbf{V}$ e sia $\mathcal{S}=\mathsf{S}(P,\mathbf{U})$ sottospazio affine di $\mathcal{A}$ ; sia $\mathbf{v} \in \mathbf{V}$ e consideriamo la traslazione $\mathsf{T}_{\mathbf{v}}$ ad esso associata; allora vale

$\begin{displaymath}\mathsf{T}_{\mathbf{v}}(\mathsf{S}(P,\mathbf{U}))=\mathsf{S}(\mathsf{T}_{\mathbf{v}}(P),\mathbf{U})\end{displaymath}$

In particolare $\mathsf{T}_{\mathbf{v}}(\mathcal{S})\parallel \mathcal{S}$ .

DIMOSTRAZIONE Procediamo alla dimostrazione della doppia inclusione:

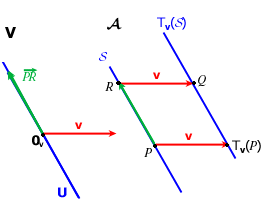
$\subseteq$ ) Sia $Q \in \mathsf{T}_{\mathbf{v}}(\mathsf{S}(P,\mathbf{U}))$ cioè $\exists\; R \in \mathsf{S}(P,\mathbf{U})$ tale che $\mathsf{T}_{\mathbf{v}}(R)=Q$ (ossia $\overrightarrow{RQ}\;=\mathbf{v}$ ); d'altra parte $R \in \mathsf{S}(P,\mathbf{U})$ vuol dire che $\overrightarrow{PR}\; \in \mathbf{U}$ e queste sono le nostre ipotesi.
Noi vogliamo dimostrare che $Q \in\mathsf{S}(\mathsf{T}_{\mathbf{v}}(P),\mathbf{U})$ cioè $\overrightarrow{\mathsf{T}_{\mathbf{v}}(P)Q} \in \mathbf{U}$ .
Il disegno ci suggerisce di provare che $\overrightarrow{\mathsf{T}_{\mathbf{v}}(P)Q}= \overrightarrow{PR}$ infatti

$\begin{displaymath}\overrightarrow{\mathsf{T}_{\mathbf{v}}(P)Q}=\overrightarrow{... ...=-\mathbf{v}+\overrightarrow{PR}+\mathbf{v}=\overrightarrow{PR}\end{displaymath}$

)

Viceversa se $M \in \mathsf{S}(\mathsf{T}_{\mathbf{v}}(P),\mathbf{U})$ cioè $\overrightarrow{\mathsf{T}_{\mathbf{v}}(P)M} \in \mathbf{U}$ , vorremmo mostrare che $M \in \mathsf{T}_{\mathbf{v}}(\mathsf{S}(P,\mathbf{U}))$ , cioè trovare $N \in \mathsf{S}(P,\mathbf{U})$ tale che $\mathsf{T}_{\mathbf{v}}(N)=M$ , ossia $\overrightarrow{NM}=\mathbf{v}$ .
La figura di nuovo ci suggerisce un candidato per

sia $N \in \mathsf{S}(P,\mathbf{U})$ tale che $\overrightarrow{PN}=\overrightarrow{\mathsf{T}_{\mathbf{v}}(P)M}$ (possiamo trovare tale

poiché $\overrightarrow{\mathsf{T}_{\mathbf{v}}(P)M} \in \mathbf{U}$ );
affermiamo che effettivamente $\overrightarrow{NM}=\mathbf{v}$ , infatti: $\overrightarrow{NM}=\overrightarrow{NP}+\overrightarrow{P\mathsf{T}_{\mathbf{v}}(P)}+\overrightarrow{\mathsf{T}_{\mathbf{v}}(P)M}=\mathbf{v}$ essendo il primo e il terzo addendo opposti.

______

_______________

________________________