

 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

|

|
In altre parole due sottospazi sono paralleli se e solo se esiste una traslazione che porta l'uno sull'altro.
DIMOSTRAZIONE
![]() )
Sia
)
Sia
![]() e
e
![]() .
.
Poniamo
![]() ;
affermiamo che
;
affermiamo che
![]() .
.
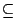 )
)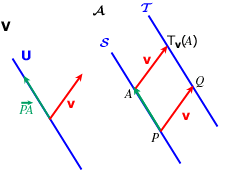 Sia
Sia 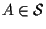 ,
cioè
,
cioè
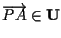 , vorremmo
, vorremmo
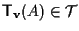 ossia
ossia
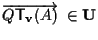 e questo è vero in quanto
e questo è vero in quanto
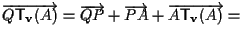
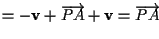 .
.
 )
)
 Se
Se 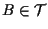 ,
cioè
,
cioè 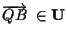 ,
vorremmo trovare
,
vorremmo trovare
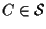 tale che
tale che
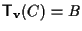 ,
cioè
,
cioè
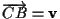 .
.
La figura ci suggerisce di prendere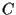 tale che
tale che
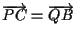 (tale
(tale 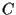 esiste unico e sta in
esiste unico e sta in
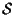 dato che
dato che
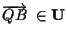 ).
).
Resta da dimostrare che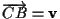 e questo è vero in quanto
e questo è vero in quanto
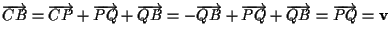 .
.
Nella proposizione precedente abbiamo determinato una traslazione che porta

 _______________
_______________
 __
__
 ________________________
________________________