5. PROPOSIZIONE Sia spazio affine su e siano e sottospazi affini di della stessa dimensione; allora

DIMOSTRAZIONE per cui se allora in virtú dell'esercizio 2.5 della sezione "Sottospazi affini".

L'inverso della proposizione in generale non è vero (per le rette nello spazio ordinario ad esempio) però è vero per le rette nel piano ordinario o per i piani nello spazio ordinario; in questi due ultimi casi abbiamo a che fare con sottospazi affini propri di dimensione massima e questa è esattamente la situazione che si presenta in generale.

6. PROPOSIZIONE Sia spazio affine su e siano e iperpiani affini di ; allora

DIMOSTRAZIONE
) È vera in generale.
) Se allora ; rimane da dimostrare
Se poniamo e abbiamo quindi per ipotesi che ; trattandosi di iperpiani vettoriali di si vede subito che (dalla formula di Grassmann vettoriale ad esempio).
Allora potremo scrivere 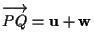con e .
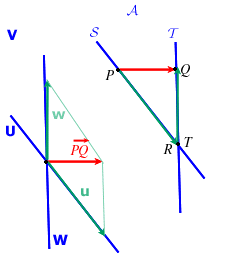
Ancora una volta la figura ci suggerisce dove trovare un punto in :
sia 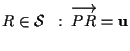e .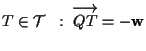
Affermiamo che e cosí possiamo concludere: .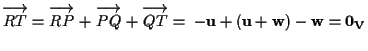

Nella figura e sono 2 rette vettoriali distinte in un piano vettoriale e quindi sono somma diretta; per cui e sono univocamente determinati e da questo deriva l'unicità del punto di intersezione di e suggerita da quella figura.
In generale e non saranno somma diretta e la possibilità di scegliere con una certa libertà e permette di trovare piú punti distinti in .

7. ESERCIZI Negli esercizi si generalizza la proposizione precedente a sottospazi arbitrari.