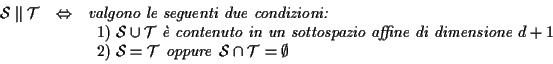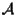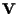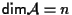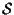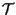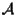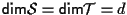7. ESERCIZIO Sia $\mathcal{A}$ spazio affine su $\mathbf{V}$, $\mathsf{dim}\mathcal{A}=n$, e siano $\mathcal{S}$ e $\mathcal{T}$ sottospazi affini di $\mathcal{A}$ con $\mathsf{dim}\mathcal{S}= \mathsf{dim}\mathcal{T}=d$, .
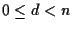Provare che:


Si noti che per definire il parallelismo fra rette dello spazio ordinario secondo l'impostazione classica della geometria elementare si procede sulla falsariga dell'esercizio precedente: nel piano due rette sono dette essere paralele se disgiunte o coincidenti e nello spazio si dà la stessa definizione per rette complanari.



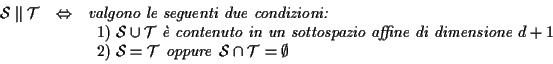
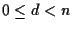vai alla soluzione, essa si aprirà in una nuova finestra torna alla teoria