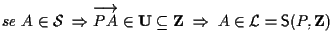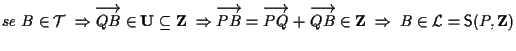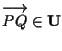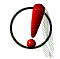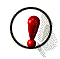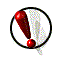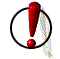7.
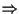 )
Poniamo
)
Poniamo
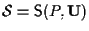 e
e
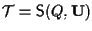 sappiamo già che vale
sappiamo già che vale 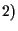 ,
dimostriamo dunque
,
dimostriamo dunque 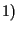 :
occorre trovare
:
occorre trovare
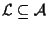 sottospazio affine di dimensione
sottospazio affine di dimensione 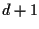 tale che
tale che
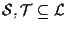 .
.
Consideriamo il vettore
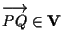 ,
si presentano due casi:
,
si presentano due casi:
- 1.
-
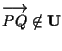

in tal caso
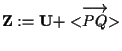 è un sottospazio vettoriale
è un sottospazio vettoriale
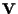 di dimensione
di dimensione 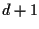 -e ciò deriva da semplici considerazioni di algebra lineare.
-e ciò deriva da semplici considerazioni di algebra lineare.
Affermiamo che
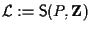 è un sottospazio affine che fa al caso nostro: ha dimensione
è un sottospazio affine che fa al caso nostro: ha dimensione 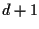 e contiene
e contiene
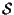 e
e
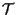 :
:
- (a)
-
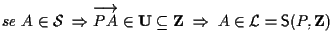
- (b)
-
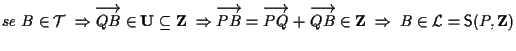
- 2.
-
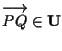
allora
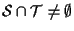 e dall'esercizio 2.5 della sezione "Sottospazi affini" scende che
e dall'esercizio 2.5 della sezione "Sottospazi affini" scende che
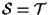 ;
a questo punto, scelto un arbitrario sottospazio vettoriale
;
a questo punto, scelto un arbitrario sottospazio vettoriale
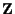 di
di
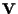 di dimensione
di dimensione 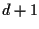 contenente
contenente
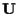 ,
affermiamo che
,
affermiamo che
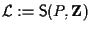 fa al caso nostro e la prova è identica a quella precedente.
fa al caso nostro e la prova è identica a quella precedente.
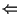 )
Se
)
Se
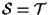 allora
allora
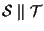 .
.
Supponiamo che
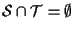 e che esista un sottospazio affine
e che esista un sottospazio affine
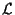
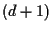 -dimensionale contenente entrambi. Allora possiamo considerare
-dimensionale contenente entrambi. Allora possiamo considerare
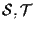 come sottospazi di
come sottospazi di
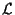 ;
visti cosí essi sono iperpiani e possiamo applicare la proposizione 6 .
;
visti cosí essi sono iperpiani e possiamo applicare la proposizione 6 .
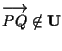

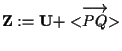 è un sottospazio vettoriale
è un sottospazio vettoriale
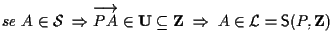
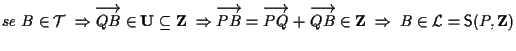
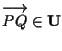
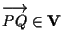 ,
si presentano due casi:
,
si presentano due casi:
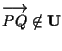

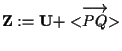 è un sottospazio vettoriale
è un sottospazio vettoriale