

 |
 |
 |
 |
 |
 |
 |
 |

|

|
9. DEFINIZIONE Sia
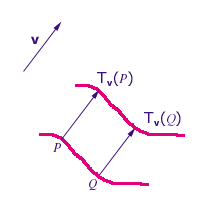 ove
ove 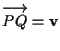 ,
è ben definita grazie ad ASS.1 ed è detta traslazione
di
,
è ben definita grazie ad ASS.1 ed è detta traslazione
di

 _______________
_______________
 __
__
 ________________________
________________________

 |  | ||||||||||||
|
9. DEFINIZIONE Sia  ove
ove 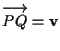 ,
è ben definita grazie ad ASS.1 ed è detta traslazione
di ,
è ben definita grazie ad ASS.1 ed è detta traslazione
di
| ||||||||||||
 |
______
 _______________ _______________
 __ __
 ________________________ ________________________

|