ASSIOMI DI SPAZIO AFFINE

1. DEFINIZIONE Sia

-spazio vettoriale; un insieme $\mathcal{A} \neq \emptyset$ è detto spazio affine su $\mathbf{V}$ se ad ogni coppia di elementi

di $\mathcal{A}$ , detti punti, possiamo associare un vettore di $\mathbf{V}$ , denotato con il simbolo $\stackrel{\displaystyle{\longrightarrow}}{PQ}$ e detto vettore di punto iniziale

e punto finale

, in modo tale che i seguenti due assiomi valgano:

ASS.1

ASS.2

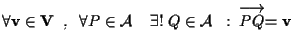
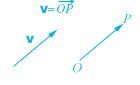
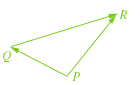
2. OSSERVAZIONE In termini piú formali possiamo dire che $\mathcal{A} \neq \emptyset$ è spazio affine su $\mathbf{V}$ se esiste un'applicazione

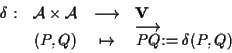
$\begin{displaymath}\begin{array}{cccl} \delta : & \mathcal{A}\times \mathcal{A}... ...{\displaystyle{\longrightarrow}}{PQ}:=\delta (P,Q) \end{array}\end{displaymath}$

con le proprietà citate sopra; si dice che $\delta$ definisce una struttura affine sull'insieme $\mathcal{A}$ .

Quindi formalmente lo spazio affine è la terna $(\mathcal{A},\mathbf{V}, \delta)$ ma noi ci riferiremo piú semplicemente all'insieme $\mathcal{A}$ sottointendendo fissata una struttura affine su $\mathcal{A}$ - a priori ce ne possono essere diverse sullo stesso insieme, ottenendo cosí diversi spazi affini.

Terminologia: Se $\mathbf{K}=\mathbf{R}$ (risp. $\mathbf{K}=\mathbf{C}$ ) $\mathcal{A}$ è detto spazio affine reale (risp. complesso).

______

_______________

_________________