SULLA DEFINIZIONE DI SPAZIO AFFINE

Ricordando quanto fatto nella sezione "Geometria affine intuitiva" e finora in questa sezione, dovrebbe essere ormai chiaro il percorso che abbiamo seguito: siamo partiti dal piano ordinario (analogamente dallo spazio ordinario) e utilizzando alcune sue proprietà di natura geometrica abbiamo

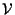costruito l'insieme $\mathcal{V}$ ;
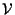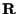provato che $\mathcal{V}$ è un $\mathbf{R}$ -spazio vettoriale di dimensione 2 (3 per lo spazio ordinario);
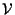determinato un'applicazione che ad ogni coppia di punti del piano ordinario associa un vettore di $\mathcal{V}$ .

Ora invece

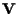$\mathbf{V}$ è preassegnato;
in particolare è preassegnata la sua struttura di spazio vettoriale (ma su un campo 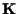$\mathbf{K}$ arbitrario, e di dimensione arbitraria);
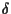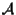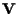cosí come è preassegnata l'applicazione $\delta$ che associa ad ogni coppia di punti di $\mathcal{A}$ un vettore di $\mathbf{V}$ .

Si noti che abbiamo inoltre preteso una qualche forma di regolarità dall'applicazione $\delta$ -ovviamente ciò è stato fatto in conformità con quanto accadeva nel piano ordinario (e nello spazio ordinario). In effetti le conseguenze degli assiomi su $\delta$ sono molto ragionevoli nel momento in cui pensiamo ad uno spazio affine come ad una generalizzazione di piano e spazio ordinario.

Oltre ad imporre condizioni sull'applicazione $\delta$ si potrebbe pensare di modificare la definizione data operando cambiamenti nella parte che riguarda lo spazio $\mathbf{V}$ .
Si potrebbe pensare di indebolire la definizione richiedendo $\mathbf{V}$ spazio vettoriale su un corpo $\mathbf{K}$ anziché su un campo $\mathbf{K}$ -siccome un campo è anche un corpo avremmo allargato la classe degli spazi affini e il confronto tra gli spazi affini di un tipo e dell'altro riveste un grande interesse geometrico.
Oppure si potrebbe rafforzare la definizione richiedendo per $\mathbf{V}$ proprietà condivise da $\mathcal{V}$ , ad esempio richiedere $\mathbf{K}$ infinito (come è $\mathbf{R}$ ) o $\mathbf{K}$ ordinato (come è $\mathbf{R}$ ) o proprio $\mathbf{K}=\mathbf{R}$ -questa volta restringeremmo la classe degli spazi affini mantenendo comunque tra essi il piano e lo spazio ordinario.
Ancora ci si potrebbe limitare a scegliere $\mathbf{V}$ di dimensione 2 (come lo spazio dei vettori liberi associato al piano ordinario) o di dimensione 3 (come lo spazio dei vettori liberi associato allo spazio ordinario).
È interessante notare, possiamo anticiparlo fin d'ora, che se si sceglie $\mathbf{K}=\mathbf{R}$ e $\mathsf{dim}\mathbf{V}=2$ (rispettivamente ) non si ottiene in realtà nessuna generalizzazione rispetto al piano ordinario (rispettivamente spazio ordinario) nel senso che non esistono modelli di spazi affini ''sostanzialmente'' diversi da questo.

In definitiva in uno spazio affine ci aspettiamo di ritrovare tutti quei concetti e quelle proprietà di natura geometrica che ci hanno permesso di costruire $\mathcal{V}$ nel piano ordinario (e nello spazio ordinario) e questo è quanto andremo a fare.

______

_______________

________________________