DEFINIZIONE DI SPAZIO AFFINE: INTRODUZIONE

Nella sezione "Geometria affine intuitiva" abbiamo associato al piano ordinario $\Pi$ gli spazi vettoriali dei vettori applicati e lo spazio vettoriale $\mathcal{V}$ dei vettori liberi (ottenendo $\mathbf{R}$ -spazi vettoriali di dimensione due). Abbiamo accennato a come costruzioni del tutto analoghe possano venir eseguite anche per lo spazio ordinario $\Upsilon$ (ottenendo in tal caso $\mathbf{R}$ -spazi vettoriali di dimensione tre).

Se fissiamo un punto $O \in \Pi$ è immediato riconoscere che l'applicazione

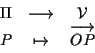
$\begin{displaymath}\begin{array}{ccc} \Pi & \longrightarrow & \mathcal{V} \\ ... ...sto & \stackrel{\displaystyle{\longrightarrow}}{OP} \end{array}\end{displaymath}$

è una biezione che ci permette di identificare i punti di $\Pi$ e i vettori di $\mathcal{V}$ , ed evidentemente dipende da

A questo punto il lettore dovrebbe obbiettare dicendo che questa procedura va contro lo spirito con cui introducemmo lo spazio $\mathcal{V}$ , cioè associare al piano ordinario uno spazio vettoriale che non dipenda dalla scelta di un punto del piano ordinario stesso, nel quale per sua natura non vi è un punto privilegiato rispetto agli altri. A tal fine sarebbe bastato considerare la biezione

$\begin{displaymath}\begin{array}{ccc} \Pi & \longrightarrow & \mathcal{V}_{O} \\ P & \mapsto & (O,P) \end{array}\end{displaymath}$

e in effetti , una volta che si è fissato un punto

, si ha la biezione

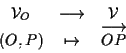
$\begin{displaymath}\begin{array}{ccc} \mathcal{V}_{O} & \longrightarrow & \math... ...sto & \stackrel{\displaystyle{\longrightarrow}}{OP} \end{array}\end{displaymath}$

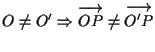
In definitiva abbiamo che, dato $P \in \Pi$ , il vettore libero $\stackrel{\displaystyle{\longrightarrow}}{OP}$ dipende dalla scelta di : e ciò ci dovrebbe convincere che non è possibile "vedere" il piano ordinario come uno spazio vettoriale in modo intrinseco, cioè poter considerare in modo canonico ogni punto di $\Pi$ come un vettore (proprio perché in ogni spazio vettoriale $\mathbf{V}$ un elemento "particolare" c'è: $\mathbf{0}_{\mathbf{V}}$ ).

Dobbiamo accontentarci di meno, cioè della costruzione (intrinseca) dello spazio $\mathcal{V}$ , e dunque in ultima analisi del fatto di poter associare ad ogni coppia di punti $P,Q \in \Pi$ un vettore, $\stackrel{\displaystyle{\longrightarrow}}{PQ}$ , di $\mathcal{V}$ .

Si noti come valga

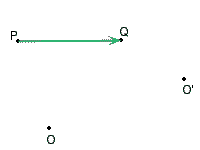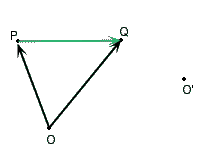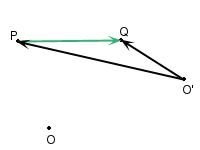
cioè sono queste differenze ad essere indipendenti dalla scelta di .

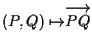Nella definizione astratta di uno spazio affine $\mathcal{A}$ che stiamo per dare invertiremo il punto di vista: preassegneremo uno spazio vettoriale $\mathbf{V}$ e l'associazione $(P,Q) \mapsto \stackrel{\displaystyle{\longrightarrow}}{PQ}$ che determina un vettore data una coppia di punti di $\mathcal{A}$ . Alcune proprietà, verificabili in modo geometrico intuitivo, che questa associazione aveva nel piano ordinario saranno ora prese come assiomi di partenza.

______

_______________

________________________