OPERAZIONI TRA VETTORI LIBERI

Dotiamo $\mathcal{V}$ della struttura di $\mathbf{R}$ -spazio vettoriale: a tal fine dobbiamo definire le operazioni di addizione e moltiplicazione per uno scalare.

7. DEFINIZIONE
Somma: Siano $\mbox{\textbf{v,w}}\in \mathcal{V}$ ; fissiamo un punto $O\in \Pi$ , ciascuno dei due vettori liberi ha un unico rappresentante in $\mathcal{V}_{O}$ ; siano essi e rispettivamente; noi sappiamo sommare tali vettori applicati di $\mathcal{V}_{O}$ ; sia tale somma; poniamo $\mbox{\textbf{z}}:=\stackrel{\displaystyle{\longrightarrow}}{OR}$ cioè $\mbox{\textbf{z}}$ è il vettore libero di cui è un rappresentante, definiamo $\mbox{\textbf{v}}+\mbox{\textbf{w}}:=\mbox{\textbf{z}}$ .

Prodotto per uno scalare: Siano $\mbox{\textbf{v}}\in \mathcal{V}$ e $\lambda \in \mbox{\textbf{R}}$ ; fissiamo ancora un punto $O\in \Pi$ ; $\mbox{\textbf{v}}$ ha un unico rappresentante in $\mathcal{V}_{O}$ ; sia esso ; noi sappiamo moltiplicare questo vettore appl. per il numero reale $\lambda$ : sia il risultato di tale operazione;
poniamo $\mbox{\textbf{z}}:=\stackrel{\displaystyle{\longrightarrow}}{OR}$ e definiamo $\lambda \mbox{\textbf{v}}:=\mbox{\textbf{z}}$ .

In definitiva abbiamo sfruttato semplicemente le operazioni già definite negli spazi dei vettori applicati (ci siamo ricondotti al... caso precedente); d'altra parte dopo aver operato in tale maniera ci si deve porre questa domanda: quello che abbiamo ottenuto dipende o meno dalla scelta dei rappresentanti? Cioè il vettore $\mbox{\textbf{v}}+\mbox{\textbf{w}}$ e il vettore $\lambda \mbox{\textbf{v}}$ dipendono dalla scelta del punto Se accadesse questo chiaramente la precedente definizione sarebbe scorretta; fortunatamente tutto funziona bene, come il lettore può facilmente verificare con l'ausilio di qualche disegno.

Con le operazioni definite sopra $\mathcal{V}$ è un $\mathbf{R}$ -spazio vettoriale di dimensione 2, ciò si prova facilmente sfruttando il fatto che $\mathcal{V}_{O}$ lo è.

8. OSSERVAZIONE Si osservi che per ogni terna di punti $L,M,R \in \Pi$ si ha

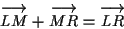
$\begin{displaymath}\stackrel{\displaystyle{\longrightarrow}}{LM}+\stackrel{\disp... ...tarrow}}{MR}\;=\;\stackrel{\displaystyle{\longrightarrow}}{LM} \end{displaymath}$

______

_______________

________________________