Per motivare la definizione astratta di spazio affine che sarà data, cominciamo col ricordare le connessioni che esistono tra piano e spazio ordinario e gli spazi vettoriali. Per fissare le idee riferiamoci al piano ordinario.

Noi supponiamo che il lettore sappia già cos'è un -spazio vettoriale; un tal lettore avrà già senz'altro visto come esempio di -spazio vettoriale lo spazio dei vettori del piano ordinario applicati in un punto; qui richiamiamo questo esempio perché ci serve per introdurre i vettori liberi.

1. DEFINIZIONE   Fissiamo un punto nel piano ordinario; in questo modo possiamo costruire in 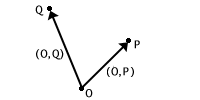modo naturale uno spazio vettoriale su di dim. 2 chiamando vettori applicati in tutte le coppie ordinate del tipo ove è un punto del piano ordinario stesso; denotiamo tale insieme con il simbolo .

Rappresentiamo graficamente questi vettori come frecce o segmenti orientati con la punta nel secondo estremo. La scelta di una freccia si spiega in quanto dobbiamo rappresentare una coppia ordinata di punti e non un semplice insieme costituito da 2 punti.

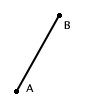
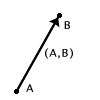
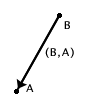
Inoltre osserviamo che nella nostra rappresentazione grafica del vettore applicato coinvolgiamo tutti i punti che "stanno tra" e ; in effetti si tratta di una pura comodità grafica visto che tali punti sono determinati univocamente dagli estremi.