Abbiamo detto che ha una naturale struttura di spazio vettoriale su ; per attribuire significato alla precedente asserzione dobbiamo però definire le operazioni di addizione fra due vettori applicati (in ) e di moltiplicazione di un numero reale per un vettore applicato (in ).

Sfruttiamo l'efficacia della rappresentazione grafica per definire tali operazioni:

2. DEFINIZIONE  
Somma: Siano , definiamo: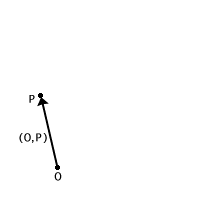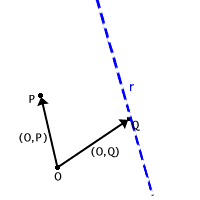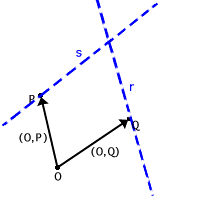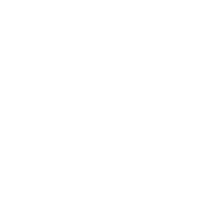
    
completiamo cioè il parallelogramma se 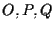non sono allineati;

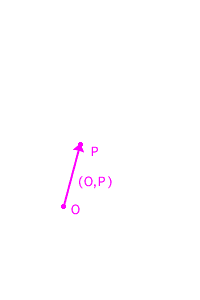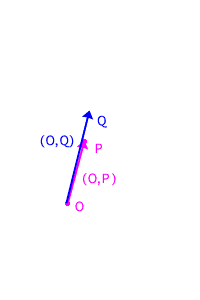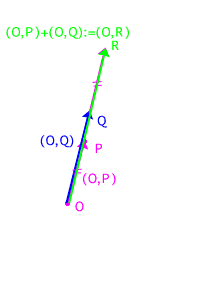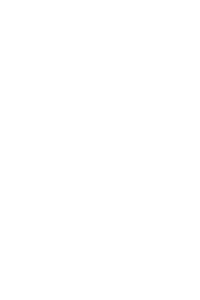Altrimenti procediamo come descritto nella figura a fianco:




  

Non è altro che il caso degenere della situazione precedente.
Prodotto per uno scalare: Se è un numero reale definiamo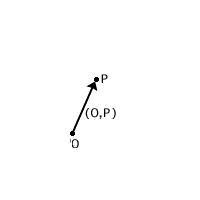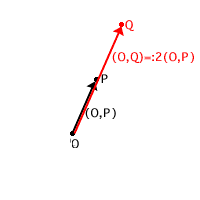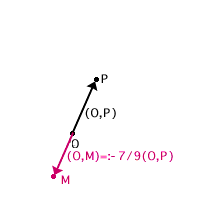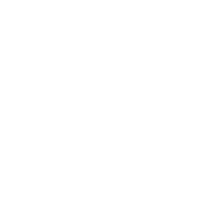





ove è ottenuto "allungando o contraendo" il segmento nella giusta direzione.

Ora "graficamente" si può verificare senza sforzo che tali operazioni inducono su una struttura di -spazio vettoriale di dim. 2.

Siamo stati volutamente approssimativi nelle definizioni precedenti, affidandoci all'intuizione geometrica del lettore.