VETTORI APPLICATI EQUIPOLLENTI

Abbiamo associato al piano ordinario lo spazio vettoriale dei vettori applicati in un punto e abbiamo visto come esso dipenda dalla scelta del punto di applicazione dei vettori; cercheremo ora di associare al piano ordinario uno spazio vettoriale "canonico", non dipendente cioè da scelte arbitrarie.

A questo scopo introduciamo il concetto di vettori applicati "equipollenti"; consideriamo l'insieme

$\begin{displaymath}\mbox{\boldmath ${\widetilde{V}}$}:=\bigcup_{O \in \Pi}\mathcal{V}_{O} \end{displaymath}$

cioè nient'altro che l'insieme di tutti i vettori applicati.

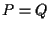4. DEFINIZIONE Siano dunque $(P,Q), (P',Q') \in \mbox{\boldmath${\widetilde{V}}$ }$ due qualsiasi vettori applicati; diciamo che sono equipollenti se:

e 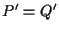oppure se
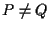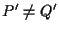$P \neq Q$ e $P' \neq Q'$ e

1.
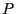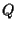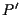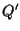la retta per e è parallela alla retta per e e
2.
il segmento 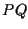è congruente al segmento 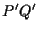-cioè hanno la stessa lunghezza-
3.
i vettori applicati 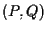e 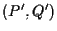hanno lo stesso verso.

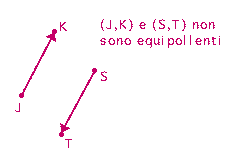
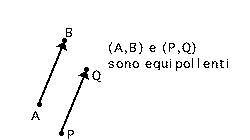
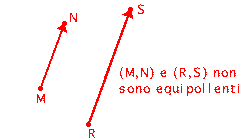
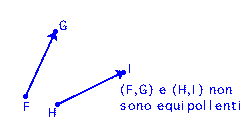
Noti il lettore che e sono equipollenti se e solo se tali due vettori si corrispondono tramite l'isomorfismo $\psi$ già descritto (vedi esercizio 3.2) tra $\mathcal{V}_{P}$ e $\mathcal{V}_{P'}$ .
A questo punto osserviamo che la relazione or ora introdotta nell'insieme $\mbox{\boldmath${\widetilde{V}}$ }$ dei vettori applicati è una relazione d'equivalenza che sarà indicata con il simbolo $\equiv$ -il lettore può verificare immediatamente questa asserzione- .

Avendo dunque una relazione di equivalenza $\equiv$ sull'insieme $\mbox{\boldmath${\widetilde{V}}$ }$ dal punto di vista matematico è naturale considerare l'insieme quoziente $\mbox{\boldmath${\widetilde{V}}$ }/ \equiv$ , l'insieme cioè delle classi di equivalenza; indichiamo tale insieme con il simbolo $\mathcal{V}$ .

______

_______________

________________________