DEFINIZIONE VETTORE LIBERO

5. DEFINIZIONE Sia dunque

un vettore applicato e consideriamo la famiglia di vettori appl. equipollenti che esso determina; indicheremo tale famiglia, pensata come elemento dell'insieme quoziente $\mbox{\boldmath${\tilde{V}}$ }/ \equiv$ , con il simbolo $\stackrel{\displaystyle{\longrightarrow}}{PQ}$ e d'ora in poi essa sarà chiamata vettore libero di cui il vettore appl.

è rappresentante.

Denoteremo i vettori liberi anche con lettere latine minuscole in grassetto.

Rappresentazione grafica di un vettore libero: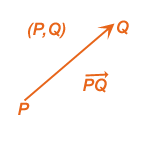
Dato che un vettore libero è un insieme di vettori applicati, e abbiamo già detto come si rappresentano graficamente i vettori applicati, l'idea piú logica sarebbe quella di rappresentare graficamente tutti i vettori applicati che costituiscono un vettore libero. Ciò però si dimostra immediatamente non molto pratico... finiremmo per riempire il foglio a nostra disposizione. In effetti basta limitarsi a rappresentare graficamente un solo vettore applicato (cioè a scegliere un rappresentante), il contesto del discorso e le notazioni ci chiariranno se ci stiamo riferendo a quel particolare vettore appl. o al vettore libero che esso individua.

6. OSSERVAZIONE Si osservi inoltre che un vettore libero ammette un unico rappresentante in ogni insieme $\mathcal{V}_{O}$ . L'analogo di questo fatto, ora evidente, verrà postulato quando tratteremo gli spazi affini in modo assiomatico.

A questo punto dovrebbe essere chiaro quanto viene fatto nella scuola superiore in cui si definiscono i vettori (applicati) come segmenti orientati e poi si permette loro di "muoversi rigidamente parallelamente a se stessi" cioè di "traslare" (passando cosí al concetto di vettore libero!!).

______

_______________

________________________