TORNA ALLA HOME PAGE TORNA ALL'ELENCO DELLE SEZIONI






precedente
successivo

7. PROPOSIZIONE
1.
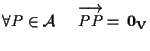
$\forall P \in \mathcal{A} \;\;\;\; \stackrel{\displaystyle{\longrightarrow}}{PP}\: = \: \mathbf{0}_{\mathbf{V}}$
infatti da ASS.2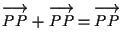 $\stackrel{\displaystyle{\longrightarrow}}{PP}+\stackrel{\displaystyle{\longrightarrow}}{PP}\: = \: \stackrel{\displaystyle{\longrightarrow}}{PP}$ da cui la tesi (si è usato il fatto che 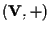$(\mathbf{V},+)$ è un gruppo).
2.
                
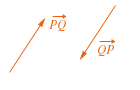
infatti da ASS.2 , da cui, utilizzando punto 1, otteniamo da cui la tesi.
3.
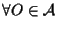$\forall O \in \mathcal{A}$ l'applicazione


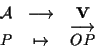
è una biezione.

Questo è infatti esattamente il contenuto di ASS.1

.


8. ESERCIZI Negli esercizi si esaminano altre semplici conseguenze degli assiomi.vai agli esercizi

MAPPA DEL SITO ______ vai in cima alla pagina_______________ precedente__ successivo________________________