 |
 |
 |
 |
|
 |
 |
 |
|
|
10. PROPOSIZIONE Sia
spazio affine su
;
sia
;
è
biunivoca.
DIMOSTRAZIONE Dobbiamo dimostrare che
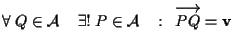e questo è il risultato dell'esercizio 8.2 della presente sezione.
11. PROPOSIZIONE Sia
spazio affine su
;
siano
;
allora
tale che
;
in altre
parole una traslazione è univocamente determinata dall'immagine di
un suo punto.
DIMOSTRAZIONE
)
Supponiamo che
esista; allora si ha
che 
per cui
è univocamente determinato.
)
Proviamo che
è una (e quindi la) traslazione che fa al caso nostro, cioè
e ciò è
tautologico.12. ESERCIZI Negli esercizi si esaminano altre proprietà delle traslazioni che talvolta ci torneranno utili.
_______________
__
________________________