|
|

|

|
Vogliamo ora motivare la definizione di sottospazio affine che andremo a dare: consideriamo lo spazio ordinario 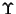 ;
sappiamo che, scegliendo un punto ;
sappiamo che, scegliendo un punto
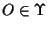 ,
possiamo costruire lo spazio vettoriale ,
possiamo costruire lo spazio vettoriale
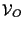 dei vettori applicati in
dei vettori applicati in 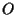 ;
consideriamo i sottospazi vettoriali di ;
consideriamo i sottospazi vettoriali di
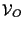 :
abbiamo :
abbiamo
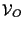 stesso e
stesso e
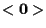 ;
se identifichiamo un vettore applicato ;
se identifichiamo un vettore applicato 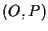 con il punto
con il punto 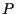 -avendo ben chiaro in mente che è stato fissato un punto
-avendo ben chiaro in mente che è stato fissato un punto 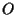 - potremo considerare i sottospazi precedenti come sottoinsiemi di - potremo considerare i sottospazi precedenti come sottoinsiemi di 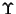 ,
precisamente essi corrispondono rispettivamente a tutto ,
precisamente essi corrispondono rispettivamente a tutto 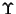 e
e  . .
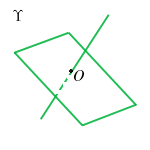
Analogamente è noto che i sottospazi vettoriali di dimensione 1 e 2 di
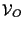 corrispondono rispettivamente alle rette e piani (nel senso della geometria elementare) di
corrispondono rispettivamente alle rette e piani (nel senso della geometria elementare) di 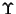 passanti per il punto
passanti per il punto 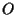 . .
Chiaramente in questo modo non consideriamo tutti gli "oggetti" interessanti di 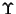 :
non tutte le rette e piani (nel senso della geometria elementare) passano per :
non tutte le rette e piani (nel senso della geometria elementare) passano per 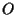 . .
Per risolvere il problema si può pensare di agire in due modi (in realtà del tutto equivalenti tra loro).
Potremmo osservare che ogni retta (risp. piano) è il traslato di un'unica retta (risp. piano) passante per l'origine.

Potremmo osservare che, data una retta (risp. piano) di 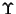 ,
essa potrà essere considerata sottospazio vettoriale di un qualsiasi spazio ,
essa potrà essere considerata sottospazio vettoriale di un qualsiasi spazio
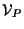 dei vettori applicati in un suo qualche punto
dei vettori applicati in un suo qualche punto 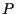 . .
Abbiamo cioè bisogno di considerare "simultaneamente" i diversi spazi di vettori applicati e potremo far ciò considerando lo spazio
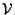 . .
Geometricamente i sottospazi vettoriali di
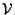 di dimensione 1 (risp. 2) corrispondono a famiglie massimali di rette (risp. piani) di
di dimensione 1 (risp. 2) corrispondono a famiglie massimali di rette (risp. piani) di 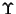 parallele fra di loro, cioè a fasci di rette (risp. piani) parallele.
parallele fra di loro, cioè a fasci di rette (risp. piani) parallele.
Ogni retta (risp. piano) di 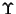 nel senso della geometria elementare sta in una e una sola di tali famiglie, per cui sarà individuata specificando la famiglia di appartenenza (cioè il sottospazio di
nel senso della geometria elementare sta in una e una sola di tali famiglie, per cui sarà individuata specificando la famiglia di appartenenza (cioè il sottospazio di
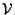 )
e un qualsiasi punto per cui essa passa. )
e un qualsiasi punto per cui essa passa.
Questo fatto geometrico ispira la definizione formale che ci permetterà di dire che cosa intendiamo per rette e piani e, piú in generale, per sottospazi affini di uno spazio affine astratto.
|












 _______________
_______________
 __
__
 ________________________
________________________