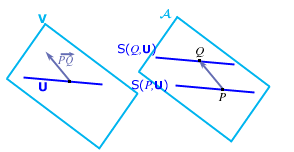
INTERSEZIONE DI SOTTOSPAZI AFFINI

L'intersezione di due sottospazi affini non è sempre un sottospazio affine, infatti, come gli esempi intuitivi di piano e spazio ordinario ci suggeriscono, essa può essere anche vuota e noi sappiamo che un sottospazio affine non è mai vuoto (esercizio 2.3).

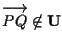Per esempio sia $\mathcal{A}$ spazio affine su $\mathbf{V}$ e sia $\mathsf{dim}\mathcal{A}=2$ ; sia $\mathbf{U}\subseteq \mathbf{V}$ una retta vettoriale; siano $P,Q \in \mathcal{A}$ tali che $\stackrel{\displaystyle{\longrightarrow}}{PQ}\; \not \in \mathbf{U}$ (tale scelta è certamente possibile, perché?).
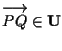Affermiamo che i sottospazi affini $\mathsf{S}(P,\mathbf{U}),\mathsf{S}(Q,\mathbf{U})$ sono disgiunti, infatti se avessero un punto in comune allora sarebbero coincidenti per esercizio 2.5, allora in particolare $\stackrel{\displaystyle{\longrightarrow}}{PQ}\; \in \mathbf{U}$ contro la nostra ipotesi.
Comunque, con l'eccezione dell'intersezione vuota, l'intersezione di sottospazi affini è un sottospazio affine come chiarito dalla seguente proposizione:

10. PROPOSIZIONE Sia $\mathcal{A}$ spazio affine su $\mathbf{V}$ e siano $\mathcal{S}=\mathsf{S}(P,\mathbf{U}),\mathcal{T}=\mathsf{S}(Q,\mathbf{W})$ sottospazi affini di $\mathcal{A}$ . Supponiamo e sia pertanto $R \in \mathcal{S} \cap \mathcal{T}$ allora vale:

in particolare

è un sottospazio affine.

DIMOSTRAZIONE Sappiamo che

hanno almeno un punto in comune

per cui coincidono in virtú di esercizio 2.5
Identicamente

per cui ci basterà dimostrare che vale

Si ha

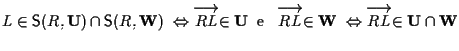
Dall'algebra lineare sappiamo che l'intersezione di due sottospazi vettoriali è sempre un sottospazio vettoriale, di qui l'affermazione che

è un sottospazio affine.

11. ESERCIZIO Nell'esercizio proposto si generalizza il contenuto della proposizione precedente per una famiglia arbitrari di sottospazi.

______

_______________

________________________