SOTTOSPAZI GENERATI DA PUNTI

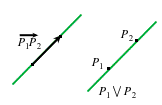
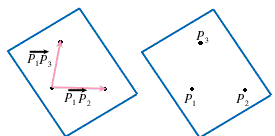
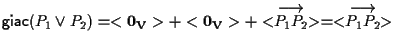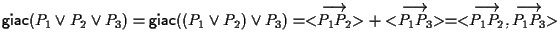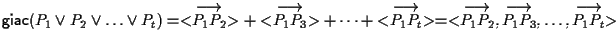17. OSSERVAZIONE SOTTOSPAZI GENERATI DA PUNTI
Sia $\mathcal{A}$ spazio affine e $P_1,\ldots,P_t\in \mathcal{A}\;,\;t \in \mathbf{N}\;,\;t \geq 1$ . Indicheremo semplicemente con il simbolo $P_1\vee\ldots \vee P_t$ il sottospazio affine somma dei sottospazi $\{P_1\},\ldots,\{P_t\}$ .
Per inciso si osservi che esso è anche il sottospazio affine generato dall'insieme $\{P_1,\ldots,P_t\}$ .

Ricordando che, se $P \in \mathcal{A}$ allora possiamo scrivere $\{P\}=\mathsf{S}(P,<\mathbf{0}_{\mathbf{V}}> )$ e utilizzando la proposizione 13 otteniamo che

In definitiva otteniamo che

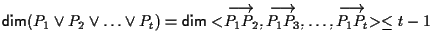
18. OSSERVAZIONE Le nozioni appena date non dipendono dall'ordine scelto per i punti nel senso che ad esempio 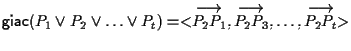$\mathsf{giac}(P_1 \vee P_2 \vee \ldots \vee P_t)=<\stackrel{\displaystyle{\long... ...htarrow}}{P_2 P_3}, \ldots, \stackrel{\displaystyle{\longrightarrow}}{P_2 P_t}>$ ove in tal caso il punto iniziale dei vettori generatori è

e non

.

19. DEFINIZIONE Sia $\mathcal{A}$ spazio affine e $P_1,\ldots,P_t\in \mathcal{A}\;,\;t \in \mathbf{N}\;,\;t \geq 1$ ; se $\mathsf{dim}(P_1 \vee \ldots \vee P_t)=t-1$ diciamo che $P_1,\ldots,P_t$ sono indipendenti o in posizione generale; altrimenti diciamo che essi sono dipendenti.

20. OSSERVAZIONE Si ha che
$P_1,\ldots,P_t$ sono punti indipendenti $\Leftrightarrow$
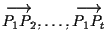$\stackrel{\displaystyle{\longrightarrow}}{P_1 P_2},\ldots,\stackrel{\displaystyle{\longrightarrow}}{P_1 P_t}$ sono vettori indipendenti $\Leftrightarrow$
$P_1,\ldots,P_t$ NON sono contenuti in un sottospazio affine

-dimensionale.

21. OSSERVAZIONE Avendo posto $\mathsf{dim}\mathcal{A}=n$ si ha:

un punto è sempre indipendente
due punti sono indipendenti se e solo se sono distinti
tre punti sono indipendenti se e solo se non giacciono su una retta (o, come si dice, non sono collineari)
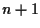punti sono indipendenti se e solo se non giacciono in un iperpiano
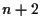o piú punti sono sempre dipendenti

22. ESERCIZI Gli esercizi esaminano alcune interessanti proprietà relative ai sottospazi generati da punti.

______

_______________

________________________