GIACITURA DEL SOTTOSPAZIO SOMMA

Già gli esempi intuitivi della pagina precedente ci fanno capire come

non dipende solo da

ma anche dalla posizione reciproca di

.

13. PROPOSIZIONE Sia $\mathcal{A}$ spazio affine su $\mathbf{V}$ e $\mathcal{S}=\mathsf{S}(P,\mathbf{U}), \mathcal{T}=\mathsf{S}(Q,\mathbf{W})$ sottospazi affini di $\mathcal{A}$ .
Allora vale

$\begin{displaymath}\mathcal{S} \vee \mathcal{T}=\mathsf{S}(P,\mathbf{U}+\mathbf{W}+<\stackrel{\displaystyle{\longrightarrow}}{PQ}>)\end{displaymath}$

DIMOSTRAZIONE Posto per semplicità 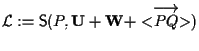procediamo alla dimostrazione della "doppia inclusione":

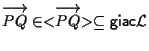$\mathcal{S} \vee \mathcal{T}\subseteq \mathcal{L}$ ): certamente $\mathcal{S} \subseteq \mathcal{L}$ poiché $\mathcal{L}\cap \mathcal{S} \neq \emptyset$ -ci sta ad esempio- e $\mathsf{giac}\mathcal{S} \subseteq \mathsf{giac}\mathcal{L}$ (vedi esercizio 9); identicamente $\mathcal{T} \subseteq \mathcal{L}$ poiché $\mathcal{L}\cap \mathcal{T} \neq \emptyset$ -ci sta ad esempio, infatti $\stackrel{\displaystyle{\longrightarrow}}{PQ}\;\in<\stackrel{\displaystyle{\longrightarrow}}{PQ}>\subseteq \mathsf{giac}\mathcal{L}$ - e di nuovo $\mathsf{giac}\mathcal{T} \subseteq \mathsf{giac}\mathcal{L}$
In definitiva $\mathcal{S} \cup \mathcal{T} \subseteq \mathcal{L}$ da cui la tesi.
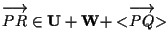$\mathcal{S} \vee \mathcal{T}\supseteq \mathcal{L}$ ): dato $R\in \mathcal{L}$ , cioè $\stackrel{\displaystyle{\longrightarrow}}{PR}\;\in \mathbf{U}+ \mathbf{W}+<\stackrel{\displaystyle{\longrightarrow}}{PQ}>$ , dobbiamo dimostrare che sta in ogni sottospazio affine contenente $\mathcal{S} \cup \mathcal{T}$ ; sia dunque $\mathcal{M}=\mathsf{S}(M,\mathsf{giac}\mathcal{M} )$ un tale sottospazio; certamente potremo scrivere $\mathcal{M}=\mathsf{S}(P,\mathsf{giac}\mathcal{M} )$ perché $P\in \mathcal{S} \subseteq \mathcal{M}$ (esercizio 2.4); a questo punto ci basta dimostrare che $\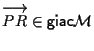stackrel{\displaystyle{\longrightarrow}}{PR}\;\in\mathsf{giac}\mathcal{M}$ ; ora certamente per ipotesi $\mathsf{giac}\mathcal{M}\supseteq\mathsf{giac}\mathcal{S}$ e $\mathsf{giac}\mathcal{M}\supseteq\mathsf{giac}\mathcal{T}$ ; inoltre affermiamo che $\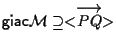mathsf{giac}\mathcal{M}\supseteq < \stackrel{\displaystyle{\longrightarrow}}{PQ}>$ infatti stanno in $\mathcal{M}$ , di qui $\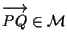stackrel{\displaystyle{\longrightarrow}}{PQ}\;\in\mathcal{M}$ (esercizio 2.1) da cui scende quanto detto.
In definitiva abbiamo che 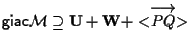$\mathsf{giac}\mathcal{M}\supseteq \mathbf{U}+\mathbf{W}+<\stackrel{\displaystyle{\longrightarrow}}{PQ}>$ in particolare contiene $\stackrel{\displaystyle{\longrightarrow}}{PR}$ .

______

_______________

________________________