DIMENSIONE DEL SOTTOSPAZIO SOMMA

14. COROLLARIO Sia $\mathcal{A}$ spazio affine e $\mathcal{S}=\mathsf{S}(P,\mathbf{U}), \mathcal{T}=\mathsf{S}(Q,\mathbf{W})$ sottospazi affini di $\mathcal{A}$ ; vale

$\begin{displaymath}\mathsf{dim}(\mathcal{S}\vee\mathcal{T})=\left\{\begin{array}... ... &\mathcal{S} \cap \mathcal{T}=\emptyset \end{array} \right. \end{displaymath}$

DIMOSTRAZIONE Sappiamo che vale

da proposizione 13.

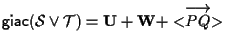
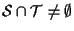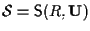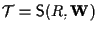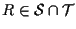I caso $\mathcal{S} \cap \mathcal{T}\neq \emptyset$ : allora potremo scrivere $\mathcal{S}=\mathsf{S}(R,\mathbf{U})$ e $\mathcal{T}=\mathsf{S}(R,\mathbf{W})$ ove $R \in \mathcal{S} \cap \mathcal{T}$ (esercizio 2.4).
A questo punto osserviamo che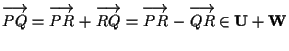 $\stackrel{\displaystyle{\longrightarrow}}{PQ}\;=\;\stackrel{\displaystyle{\long... ...}}{PR}-\stackrel{\displaystyle{\longrightarrow}}{QR}\;\in \mathbf{U}+\mathbf{W}$ dato che $\stackrel{\displaystyle{\longrightarrow}}{PR}\;\in \mathbf{U}$ e $\stackrel{\displaystyle{\longrightarrow}}{QR}\;\in \mathbf{W}$ ; di qui $\stackrel{\displaystyle{\longrightarrow}}{PQ}\; \in \mathbf{U}+\mathbf{W}$ e $\mathbf{U}+\mathbf{W}+<\stackrel{\displaystyle{\longrightarrow}}{PQ}>\subseteq \mathbf{U}+\mathbf{W}$ , e in definitiva vale l'uguaglianza.

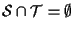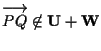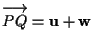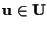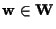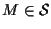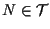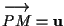II caso $\mathcal{S} \cap \mathcal{T}=\emptyset$ : ora $\stackrel{\displaystyle{\longrightarrow}}{PQ}\;\not \in \mathbf{U}+\mathbf{W}$ infatti per assurdo supponiamo di poter scrivere $\stackrel{\displaystyle{\longrightarrow}}{PQ}\;=\mathbf{u}+\mathbf{w}$ con $\mathbf{u}\in\mathbf{U}$ e $\mathbf{w}\in\mathbf{W}$ ; potremmo trovare $M \in \mathcal{S}$ e $N \in \mathcal{T}$ tali che $\stackrel{\displaystyle{\longrightarrow}}{PM}\;=\mathbf{u}$ e $\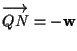stackrel{\displaystyle{\longrightarrow}}{QN}\;=-\mathbf{w}$ (vedi osservazione 8); affermiamo che 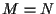contro l'ipotesi che 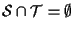$\mathcal{S} \cap \mathcal{T}=\emptyset$ infatti 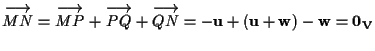$\stackrel{\displaystyle{\longrightarrow}}{MN}\;=\;\stackrel{\displaystyle{\long... ...}}{QN}\;=-\mathbf{u}+(\mathbf{u}+\mathbf{w})-\mathbf{w}=\mathbf{0}_{\mathbf{V}}$ , cioè proprio .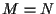
Stabilito dunque che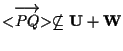 $<\stackrel{\displaystyle{\longrightarrow}}{PQ}> \not \subseteq \mathbf{U}+\mathbf{W}$ è un semplice esercizio di algebra lineare mostrare che 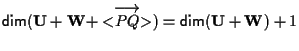$\mathsf{dim}(\mathbf{U}+\mathbf{W}+<\stackrel{\displaystyle{\longrightarrow}}{PQ}>)=\mathsf{dim}(\mathbf{U}+\mathbf{W})+1$ (basta osservare che 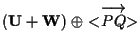, dato che ).

______

_______________

________________________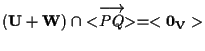