FORMULA DI GRASSMANN AFFINE

15. TEOREMA FORMULA DI GRASSMANN AFFINE
Sia $\mathcal{A}$ spazio affine su $\mathbf{V}$ e siano $\mathcal{S}=\mathsf{S}(P,\mathbf{U}),\mathcal{T}=\mathsf{S}(Q,\mathbf{W})$ sottospazi affini di $\mathcal{A}$ .
Supponiamo $\mathcal{S} \cap \mathcal{T} \neq \emptyset$ , allora per la dimensione di $\mathcal{S} \cap \mathcal{T}$ si ha la formula:

La formula precedente presuppone che si conosca la nozione di sottospazio affine somma (vedi definizione 12 e notazioni successive); altrimenti ci di può riferire alla seguente, equivalente, riscritta in termini piú familiari di giaciture come segue:

$\begin{displaymath}\mathsf{dim}(\mathcal{S} \cap \mathcal{T})= \mathsf{dim}\mat... ...sf{dim}\mathcal{T}-\mathsf{dim}(\mathbf{U+W})\;\;\;\;(\ast\ast)\end{displaymath}$

DIMOSTRAZIONE La proposizione 10 ci garantisce che, essendo $\mathcal{S} \cap \mathcal{T} \neq \emptyset$ , allora tale intersezione è un sottospazio affine per giacitura $\mathbf{U} \cap \mathbf{W}$ ; di qui $\mathsf{dim}(\mathcal{S} \cap \mathcal{T})=\mathsf{dim}(\mathbf{U} \cap \mathbf{W})$ per definizione di dimensione.
Sfruttando la formula di Grassmann vettoriale che dice che

$\begin{displaymath}\mathsf{dim}(\mathbf{U} \cap \mathbf{W})=\mathsf{dim}\mathbf{U}+\mathsf{dim}\mathbf{W}-\mathsf{dim}(\mathbf{U+W})\end{displaymath}$

e ricordando che per definizione $\mathsf{dim}\mathcal{S}=\mathsf{dim}\mathbf{U}$ e $\mathsf{dim}\mathcal{T}=\mathsf{dim}\mathbf{W}$ , otteniamo la formula $(\ast)$ .

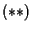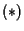A questo punto possiamo utilizzare il corollario14 per concludere che $\mathsf{dim}(\mathcal{S} \vee \mathcal{T})=\mathsf{dim}(\mathbf{U+W})$ visto che per ipotesi $\mathcal{S} \cap \mathcal{T}$ non è vuoto, ottenendo cosí $(\ast\ast)$ .

16. ESERCIZI Gli esercizi esaminano due interessanti corollari della formula di Grassmann.

______

_______________

________________________